Метод гаусса в mathcad

БлогNot. Основные прямые и итерационные методы решения СЛАУ в MathCAD

Основные прямые и итерационные методы решения СЛАУ в MathCAD

Как известно, решение систем линейных алгебраических уравнений (СЛАУ) – весьма распространённый на практике тип задач. Теорию можно почитать по ссылке, а здесь приведём основные расчёты как для прямых (аналитических), так и для итерационных (приближённых) методов решения СЛАУ.

Начнём с прямых. Классический метод обратной матрицы в MathCAD легко реализовать с помощью стандартной функции lsolve или же посредством операции обращения матрицы, код приводить не будем из-за его тривиальности.

Уже двое спросили "а как всё же найти решение методом обратной матрицы?" 🙂
Введя данные, как на картинке ниже, под данными написать одну из формул x:=A -1 *b или x:=lsolve(A,b)
Затем ещё ниже сделать x=

А вот метод Крамера запрограммируем. Элемент вектора решения x_i в нём получается в виде дроби, знаменателем которой является определитель матрицы системы, а числителем – определитель матрицы A_i , полученной из исходной заменой i-го столбца столбцом свободных членов b . Для удобства будем во всём документе нумеровать строки и столбцы матриц с единицы, то есть, установим значение системной переменной ORIGIN:=1 . Также определим общие для всех методов матрицу и вектор правой части системы:

Условием существования и единственности решения СЛАУ во всех случаях является условие det A≠0 , т.е., определитель матрицы A не равен нулю. Также имеет смысл сделать проверку полученного решения, посчитав значение невязки, равное норме разности векторов A*x ( x – найденное решение) и b . В идеале невязка должна быть равной нулю, но из-за неизбежного накопления погрешностей операций над вещественными числами она окажется равна малому числу ε , соответствующему погрешности метода. В MathCAD скалярный оператор "модуль" с панели инструментов калькулятора в применении к разности векторов даст как раз значение невязки, проверим это утверждение на небольшом тесте:

С учётом всего сказанного, реализуем метод Крамера и проверку полученного решения:

В теле функции det – не модуль, а похожая внешне кнопка "Определитель" с панели "Матрицы"!

Классический метод Гаусса с приведением матрицы к верхнему треугольному виду подробно изучается в базовом курсе высшей математики. Реализуем самую простую его разновидность, выбирающую ведущий элемент на главной диагонали матрицы, то есть, работающую в предположении, что значение A_1,1,≠0 . Так как эта подпрограмма "нулевого" уровня, назовём её Gauss0 , а более сложную Gauss напишем отдельно.

Для удобства вектор правой части b записан как (n+1) -й столбец матрицы A , такую матрицу системы называют расширенной.

Реализация более "полноценного" метода Гаусса с выбором ведущего элемента (и перестановкой при необходимости строк матрицы) выполнена в приложенном к статье документе MathCAD, по крайней мере, систему с нулями на главной диагонали матрицы подпрограмма Gauss решила. Её дополнительный параметр – погрешность ε , начиная с которой значение |A_i,j| считается равным нулю. В случае ошибки (нет решения) подпрограмма возвращает вектор из n значений "бесконечность".

На практике нетрудно увидеть общие для всех прямых методов недостатки подхода – трудоёмкость вычислений, требующая брать обратные матрицы или считать определители, следующее из неё довольно быстрое накопление погрешности, наконец, невозможность найти решение с заранее заданной, а не заложенной в алгоритм точностью.

В определённой мере избежать этих недостатков позволяют итерационные методы, последовательно приближающие решение формулами вида x_i (k+1) = f(x_i (k) ) , где k=0,1. – номер шага, до тех пор, пока выбранная мера разности между двумя соседними векторами приближениямй |x (k+1) -x (k) | не станет меньше заданного малого значения ε . В простейшем случае решение СЛАУ с матрицей размерности 2*2 методом Якоби (он же – метод простых итераций) будет выглядеть так:

Все неизвестные значения x_i присутствуют и в левой, и в правой частях новых уравнений. Выбрав некоторый вектор начального приближения x (0) , посчитаем по нему новое приближение x (1) , затем подставим его в правые части уравнений и посчитаем x (2) и т.д. до выполнения условия сходимости. А оно, кстати, довольно просто – метод Якоби сходится, если матрица системы имеет диагональное преобладание, то есть, на главной диагонали находятся наибольшие в своих строках элементы. Наша тестовая матрица уже имеет диагональное преобладание, а в большинстве других случаев этого можно добиться, выполняя преобразования над уравнениями системы, подобные тем, что делает расширенная процедура Gauss .

Выбор вектора начального приближения x (0) на практике также обычно прост, принимают x (0) =b , то есть, вектору правой части системы. Можно и просто "занулить" вектор x (0) .

Приходим к следующей процедуре решения:

Обратите внимание, что нам пришлось "схитрить" при расчёте сумм s1 и s2 – MathCAD просто не сможет вычислить сумму с нижним пределом суммирования =1 и верхним =0 (или нижним n и верхним n-1 ). По той же причине дополнительные проверки сделаны и в процедуре Gauss .

В основной "бесконечный" цикл подпрограммы имеет смысл добавить аварийный выход оператором break , например, по выполнении 10000 шагов.

Также, в этом и следующем методе в строчке с break точнее был бы критерий выхода |max(x1-x0)|≤ε , где | | – значок модуля числа с панели калькулятора.

Итерационный метод Гаусса-Зейделя отличается от метода простых итераций лишь тем, что для подсчета i –й компоненты (k+1) –го приближения к искомому вектору решения используются уже вычисленные на этом, т.е., (k+1) –м шаге новые значения первых i–1 компонент. а не просто берётся вектор x0 целиком с предыдущего шага. В нашей подпрограмме достаточно заменить x0 на x1 в операторе расчёта суммы s1 🙂 У меня точность решения на использованном тесте выросла при этом вчетверо.

Прямые и итерационные методы решения СЛАУ: скачать документ .xmcd Mathcad 14/15 в архиве .zip (56 Кб)

P.S. И ещё про прямые "гауссоподобные" методы решения СЛАУ. Если Вам нужно не пошаговое программирование, а достаточно применения стандартных функций, есть способ проще. С помощью стандартной функции augment можно получить расширенную матрицу системы (поставив "рядом" матрицу A и вектор b ), а с помощью rref привести матрицу к ступенчатому виду с единичным базисным минором. Потом останется извлечь решение с помощью метода submatrix (последний столбец матрицы, которую вернул метод rref ).

Норма вектора |A*x-b| , как и другие нормы в статье, берётся кнопкой |x| с Калькулятора, а не похожей на неё кнопкой с панели "Матрицы".

21.09.2013, 11:24; рейтинг: 39395

Краткие теоретические сведения

В системе Mathcad возможно решение систем линейных алгебраических уравнений с комплексными коэффициентами. Любое выражение, начинающееся с цифры, Mathcad интерпретирует как число. Большинство операций в среде Mathcad по умолчанию осуществляется над комплексными числами. В Mathcad комплексное число представляется в алгебраической форме. Чтобы ввести комплексное число следует в начале ввести действительную часть комплексного числа, затем знак + или – , коэффициент перед мнимой частью (это может быть любое действительное число), а затем символ . Для ввода мнимой единицы надо нажать клавиши ,. Комплексное число можно ввести в виде обычной суммы действительной и мнимой частей или в виде выражения, содержащего мнимое число. В Mathcadе используют две встроенные константы, обозначающие мнимую единицу .

Из курса линейной алгебры известно, система линейных алгебраических уравнений (СЛАУ) имеет единственное решение, если ее матрица коэффициентов является невырожденной. Самый простой способ решения таких систем – использование алгоритма Гаусса, реализованного во встроенной функции Lsolve.

Для применения этого способа необходимо, чтобы СЛАУ была записана в матричной форме.

Для обращения к функции нужно указать два аргумента: . В функции Lsolve запрограммирован численный метод LU-разложения, основанный на алгоритме последовательных исключений Гаусса. Суть его состоит в преобразовании матрицы коэффициентов к верхнему треугольному виду, т.е. к форме, когда все элементы ниже главной диагонали матрицы являются нулевыми. Результат, выдаваемый методом Гаусса, является точным.

Расширенная матрица коэффициентов принимает вид:

Mathcad- программа решения систем линейных алгебраических уравнений с комплексными коэффициентами

В результате получили , что значения контурных токов, найденные с помощью Excel программы совпадают со значения, найденными в Mathcad программе.

Краткие теоретические сведения

Численные методы решения обыкновенных дифференциальных уравнений используются для расчета переходных процессов в электроэнергетических системах. Рекомендуемый численный метод расчета переходного процесса – метод Рунге-Кутта. Все изложение ведется под реализацию этого метода.

В качестве исходных данных задачи имеем:

1. Систему обыкновенных дифференциальных уравнений 1-го порядка, описывающую переходный процесс в электроэнергетической системе.

2. Начальные условия Коши. Под начальными условиями Коши понимают значения искомых переменных при .

3. Интервал интегрирования системы обыкновенных дифференциальных уравнений. Переходные процессы в линейных электрических цепях обычно являются быстропротекающими, длительность их составляет десятые, сотые доли секунды.

Должен быть задан шаг интегрирования . В Mathcad имеется несколько встроенных функций, которые позволяют решать задачу Коши для систем обыкновенных дифференциальных уравнений 1-го порядка:

· – метод Рунге-Кутта с фиксированным шагом ;

· – метод Рунге-Кутта с переменным шагом ;

У этих функций следующие аргументы:

-вектор начальных значений в точке размерностью ,

– начальная точка расчета,

– конечная точка расчета,

– число шагов, на которых численный метод находит решение, эта переменная однозначно определяет шаг интегрирования, он равен длине отрезка интегрирования , деленному на число , чем больше число , тем точнее найденное решение,

– векторная функция размера двух аргументов – скалярного и векторного . При этом – искомая векторная функция аргумента того же

Постановка задач 3

Основная часть 3

Системы линейных алгебраических уравнений 3

Функция lsolve 4

Функция augment 5

Функция submatrix 6

Решение СЛАУ методом Гаусса 7

Решение СЛАУ методом Крамера 8

Список использованных источников 10

Научиться решать системы линейных уравнений средствами Mathcad.

Изучить материал по линейной алгебре, необходимый для

выполнения лабораторной работы;

Изучить свойство функций lsolve, augment и submatrix в программе

Научиться применять функции lsolve, augment и submatrix в

среде Mathcad для решения систем линейных алгебраических уравнений методами Гаусса и Крамера.

Системы линейных алгебраических уравнений

Центральным вопросом вычислительной линейной алгебры является решение систем линейных алгебраических уравнений (СЛАУ), т. е. систем уравнений вида

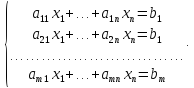
В матричной форме СЛАУ записывается в эквивалентном виде:

,

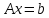где А — матрица коэффициентов СЛАУ размерности mxn;

х — вектор-столбец неизвестных;

b— вектор-столбец свободных коэффициентов.

СЛАУ имеет единственное решение, если матрица А является невырожденной, т. е. ее определитель не равен нулю.

Для упрощения решений подобных систем уравнений была создана программа Mathcad, с набором различных встроенных функций, предназначенных для решения СЛАУ, некоторые из них, такие как lsolve, augment и submatrix, мы рассмотрим далее в работе.

Функция lsolve

В Mathcad СЛАУ можно решить в более удобной для записи форме (2), с помощью функции lsolve.

Lsolve(A,b) – это встроенная функция, которая возвращает вектор x для системы линейных уравнений при заданной матрице коэффициентов А и векторе свободных членов b.

Функцию lsolve применяют в работе с Mathcad следующим образом (скриншот 1):

создается в документе требуемая СЛАУ;

опираясь на заданную СЛАУ, создаем матрицу коэффициентов –

А необходимой размерности и матрицу свободных коэффициентов – b;

в панели инструментов выбираем необходимую нам функцию –

подставляем в выбранную функцию необходимые параметры А, b;

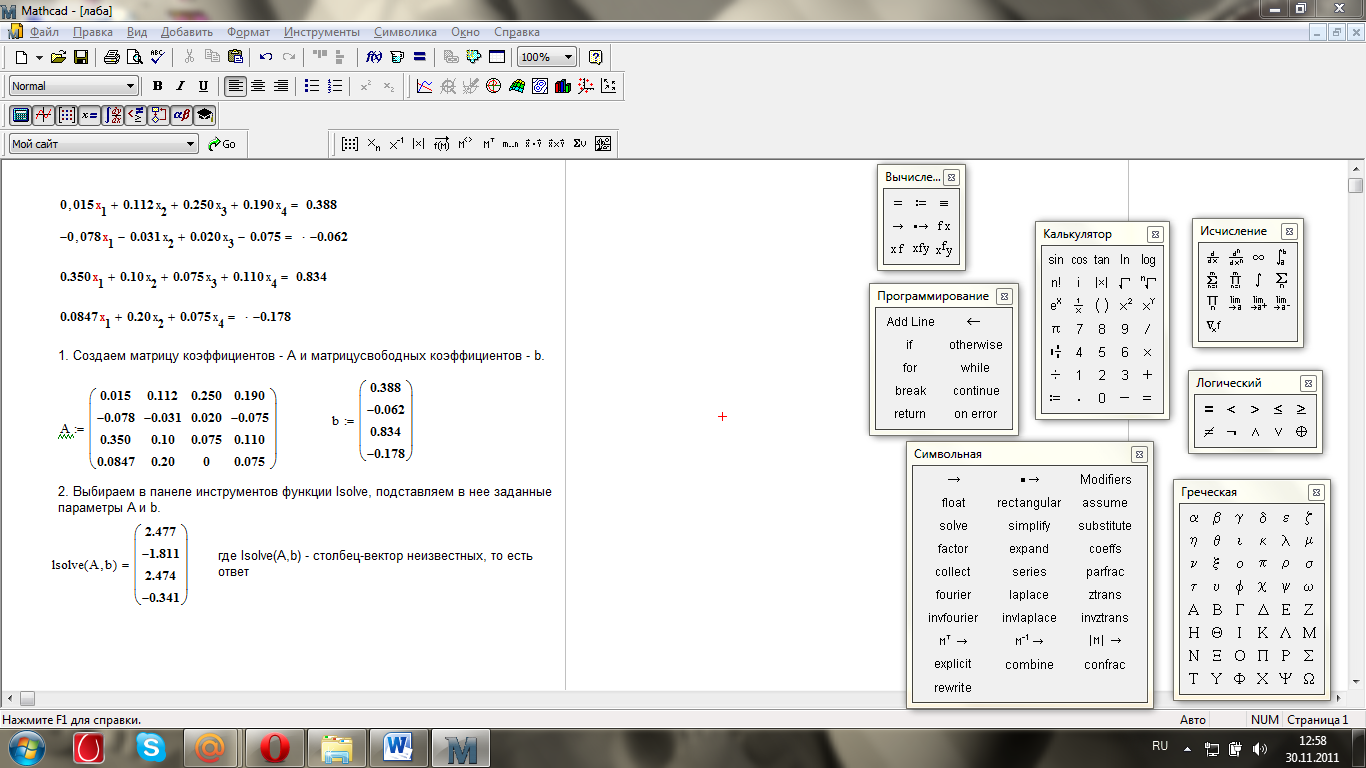
Скриншот 1 – применение функции lsolve в Mathcad

Функция augment

Функцию augment применяют для решения СЛАУ методами Крамера и Гаусса в программе Mathcad.

Аugment(A,B) – это встроенная функция, которая объединяет матрицы A и B в одну новую, при этом матрица B располагается справа от матрицы A, и обе матрицы должны иметь одинаковое число строк.

Функцию augment применяют в работе с Mathcad следующим образом (скриншот 2):

создается в документе требуемая СЛАУ;

опираясь на заданную СЛАУ, создаем матрицу коэффициентов –

А необходимой размерности и матрицу свободных коэффициентов – b, при этом матрица b должна располагаться справа от матрицы A;

в панели инструментов выбираем необходимую нам функцию –

подставляем в выбранную функцию необходимые параметры А, b;

получаем объединенную матрицу матриц A и b.

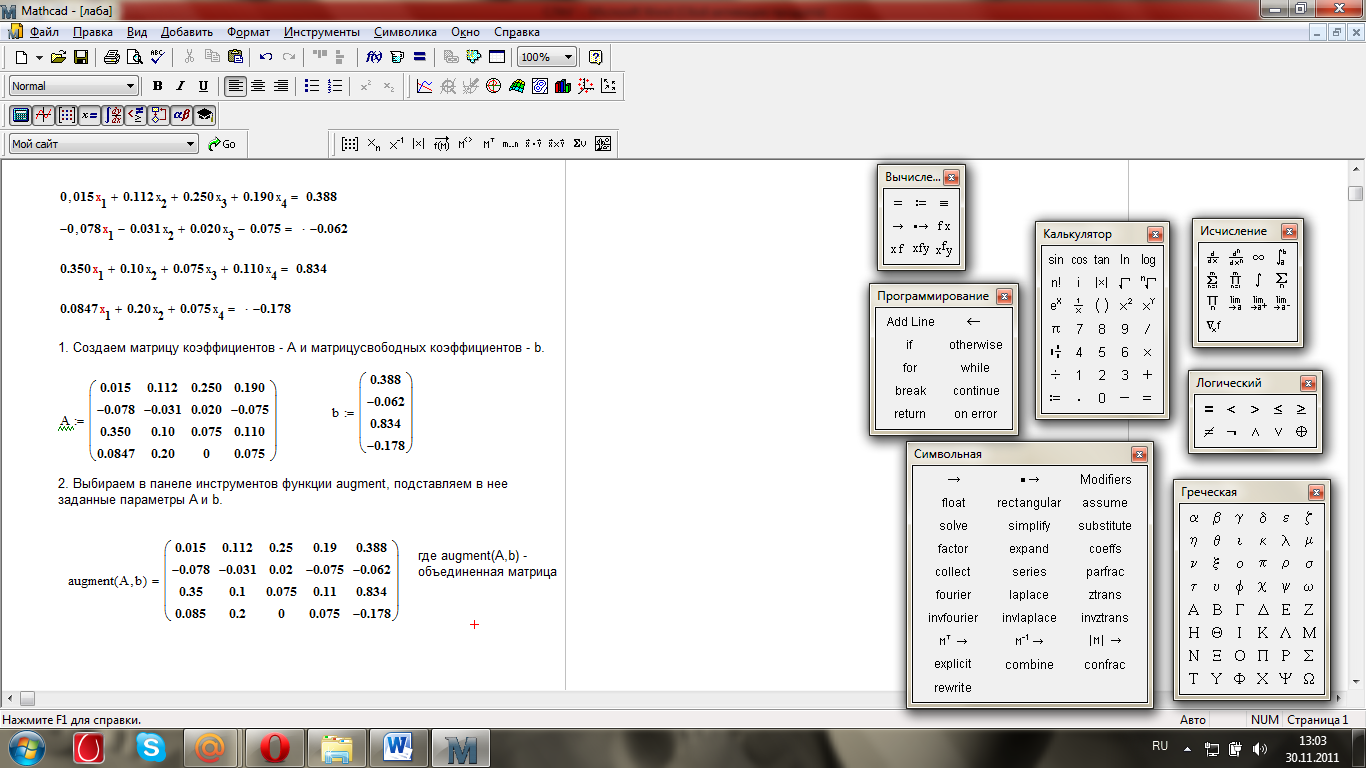
Скриншот 2 – применение функции augment в Mathcad

Функция submatrix

Функцию submatrix, также как и функцию augment и lsolve, применяют для решения СЛАУ в программе Mathcad.

Функция submatrix(А,_,_,_,_) – встроенная функция, с помощью которой можно выделить из заданной матрицы один столбец или строку.

Функцию submatrix применяют в работе с Mathcad следующим образом (скриншот 3):

создают матрицу, какой-либо размерности;

в панели инструментов выбираем необходимую нам функцию –

подставляем в выбранную функцию параметры, с помощью

значения которых мы хотим выделить столбцы или строки в новую матрицу;

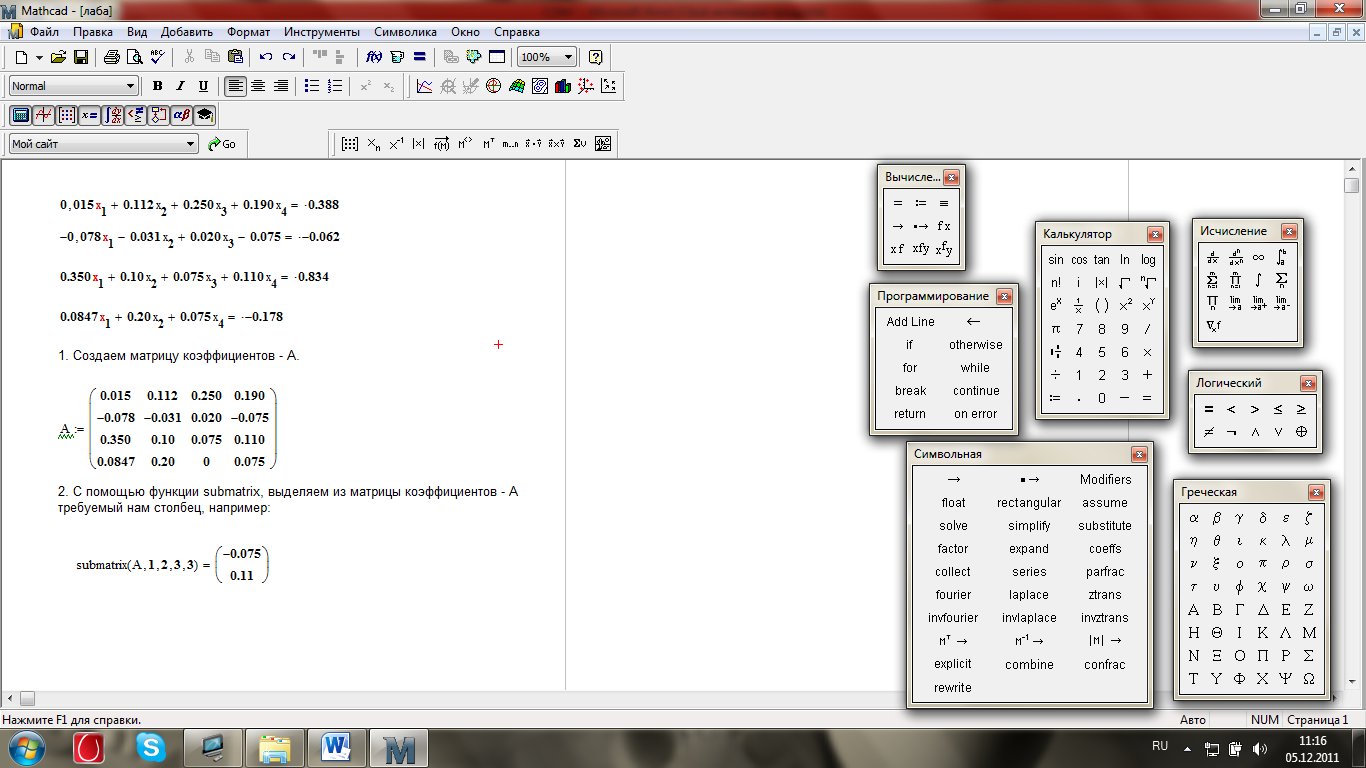
Скриншот 3 – применение функции submatrix в Mathcad

Решение СЛАУ методом Гаусса

СЛАУ в программе Mathcad можно решать не только с помощью функции lsolve, но и с помощью рассмотренных выше функций augment и submatrix, используя следующий ход вычислений (скриншот 4):

создается в документе СЛАУ;

выбрав из встроенных функций функцию ORIGIN, присваиваем ей

значение равное единице (роль данной функции заключается в том, что в последующем решении системы, в матрицах первая строка, будет иметь первый коэффициент, равный единице);

опираясь на заданную СЛАУ, создаем матрицу коэффициентов –

А необходимой размерности и матрицу свободных коэффициентов – b;

с помощь функции augment, создаем объединенную матрицу;

выбираем из встроенных функций функцию rref, и присваиваем ей

параметр, соответствующий объединенной матрице (с помощью функции rref приводим матрицу к ступенчатому виду для дальнейшего решения);

используя функцию submatrix, находим неизвестные.

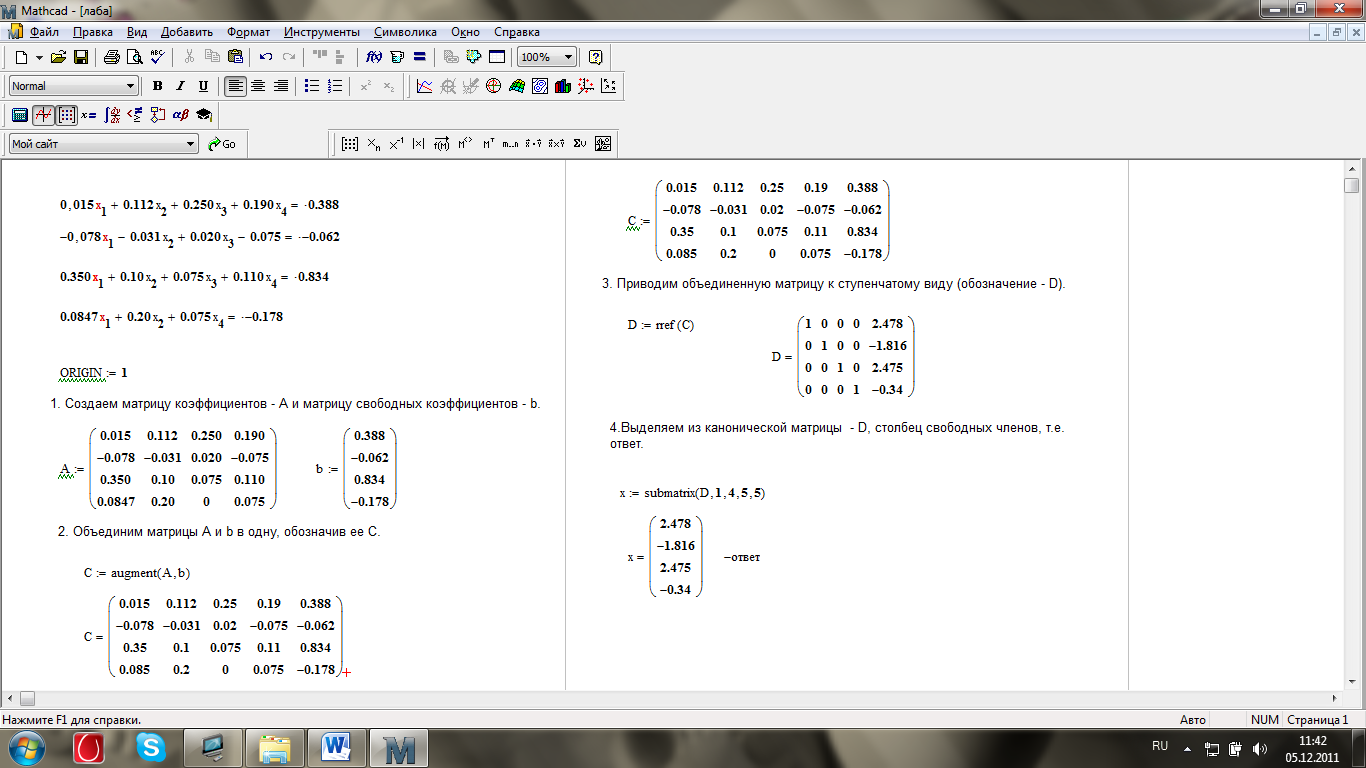
Скриншот 4 – решение СЛАУ в Mathcad методом Гаусса

Решение СЛАУ методом Крамера

СЛАУ можно решать не только методом Гаусса, но и методом Крамера. Для того чтобы произвести вычисления в программе Mathcad, достаточно двух, уже изученных нами функций: augment и submatrix.

Ход решения СЛАУ в Mathcad (скриншот 5):

создается в документе СЛАУ;

выбрав из встроенных функций функцию ORIGIN, присваиваем ей

значение равное единице;

опираясь на заданную СЛАУ, создаем матрицу коэффициентов –

А необходимой размерности и матрицу свободных коэффициентов – b;

вычисляем определитель матрицы А;

с помощью функций augment и submatrix создаем матрицы с

заменой необходимого нам столбца столбцом свободных коэффициентов – b;

вычисляем определители полученных матриц;

находим неизвестные СЛАУ по формуле Крамера:

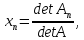
подставляя в нее полученные значения определителей.

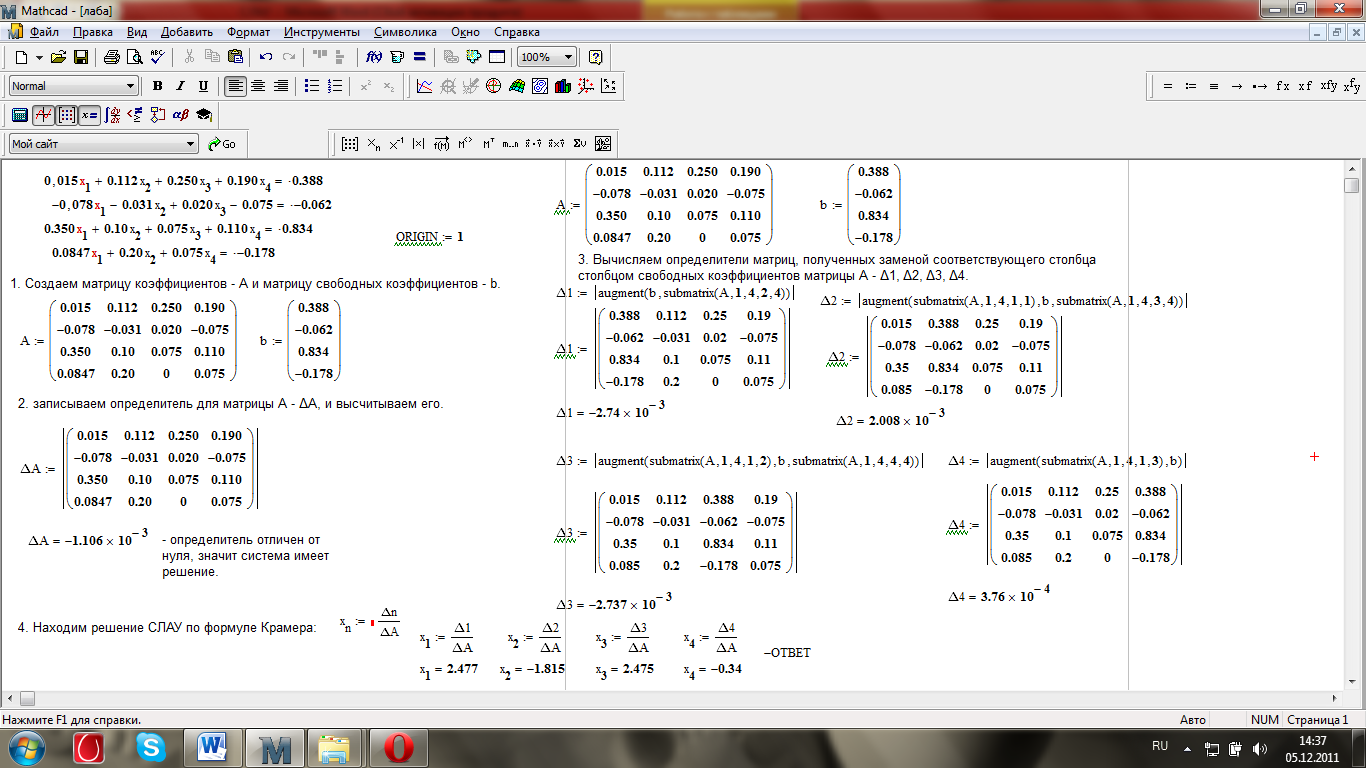
Скриншот 5 – решение СЛАУ в Mathcad методом Крамера

Программа Mathcad позволяет упростить решение СЛАУ с помощью встроенных в нее функций. Так, c помощью функции lsolve, система линейных уравнений решается в одно действие. СЛАУ методом Гаусса с помощью функций augment и submatrix решается гораздо быстрей и проще, нежели это было бы на бумаге. В данной работе были приведены решения простейших систем уравнений, которые вычислить и на бумаге не составит труда, но с помощью программы Mathcad можно решить сложнейшие системы в кротчайшее время, над решениями которых человек затратит много времени. В работе были рассмотрены всего лишь несколько функций из множества приведенных в Mathcad.

1 Плис, А. И. Mathcad: математический практикум для экономистов и инженеров: учеб. пособие/ А. И. Плис, Н. А. Сливина. – М., 1999. – 656с.

2 Панферов, А. И. Применение Mathcad в инженерных расчетах: учеб. пособие/ А. И. Панферов, А. В. Лопарев, В. К. Пономарев – М., 2004. – 88с.

3 Симонович, С. В. Информатика: базовый курс: учеб. для вузов/ С. В. Симонович – Питер, 2001. – 640с.

4 Шипачев, В. С. Высшая математика: учеб./ В. С. Шипачев – М., 1998. – 479с.

5 Черненко, В. Д. Высшая математика в примерах и задачах: учеб. пособие/ В. Д. Черненко – М., 2003. – 703с.