Метод ортогонализации решения слау

Пусть имеем систему линейных уравнений

с неособенной матрицей А. Ортогонализируя столбцы матрицы А, получим матрицу R, причем A = RT, где Т – верхняя треугольная матрица. Имеем:

Умножая слева на R / обе части равенства (2), получим:

где D – диагональная матрица. Вводя обозначение , будем иметь:

Матрица , обратная диагональной, находится легко, а именно, если

Относительно просто находится также обратная матрица Т -1 треугольной матрицы Т.

Пример 1. Методом ортогонализации столбцов решить систему уравнений

Решение. Представим матрицу А данной системы в виде произведения матрицы с ортогональными столбцами на треугольную матрицу с единичной диагональю:

По формулам (4) находим:

По формуле (4) имеем:

где диагональная матрица и

Для матрицы D и ее обратной матрицы D -1 получаем такие значения:

Обычным приемом подсчитаем:

В итоге получим:

точные значения корней:

Пусть дана система

Преобразуем строки системы (5) так, чтобы матрица А перешла в матрицу R с ортогональными строками. При этом вектор b перейдет в какой – то вектор . В результате получим эквивалентную систему

На основании формулы (7) окончательно имеем:

Используя формулу (8), можно избежать наиболее трудоемкого процесса нахождения обратной матрицы для недиагональной матрицы. Наличие матрицы D -1 не вносит усложнения, так как D – диагональная матрица.

Пример 2. Методом ортогонализации строк решить систему уравнений

Решение: Определяем множители:

Сохраняя первое уравнение системы (I), из каждого следующего вычитаем первое, умноженное на соответствующие множители

Для системы (II) определяем множитель

Сохраняя два первых уравнения системы (II), из ее третьего уравнения вычитаем второе, умноженное на множитель :

имеет ортогональные строки. Для контроля составляем матрицу

Дата добавления: 2015-01-16 ; просмотров: 4589 ; Нарушение авторских прав

Метод позволяет осуществить его реализацию при помощи чрезвычайно компактного алгоритма и компьютерной программы, не требует никаких проверок сходимости и сколько-нибудь существенных преобразований исходной системы, операция деления на коэффициенты матрицы в нем отсутствует, а имеющаяся операция деления на норму вектор-строки является намного безопасней, так как вектор нулевой длины не может присутствовать в невырожденной матрице. Все сказанное обусловило его широкое использование в прикладных задачах.

Сущность метода ортогонализации в следующем.

Перенесем свободные члены всех уравнений системы в левые части, будем считать их (n+1)-ми составляющими векторов a_i и положим x_n+1=1.

Получим систему в виде

(i=1, 2, …, n)

Суммы в левых частях уравнений можно интерпретировать как скалярные произведения векторов (a, x); в этом случае искомым решением системы будет некоторый вектор x в (n+1)-мерном пространстве, ортогональный базису, образованному системными векторами а_i.

Так как сам базис в общем случае не ортонормирован, то необходима дополнительная процедура построения системы взаимно ортогональных векторов, выражающихся линейно через исходные векторы а_i, чтобы не изменить решение системы. Выполним это так:

Первый вектор-строку образуем просто делением исходного на его длину:

b₁= .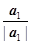

Из второго вычтем вектор, равный по длине проекции второго на направление первого:

b₂= .

Из третьего вычтем уже 2 составляющие

и отнормируем по модулю и т.д.

Добавим к векторам a_i линейно независимый от них произвольный вектор a_n+1 и, когда до него дойдет очередь, проведем с ним такую же процедуру ортогонализации всем векторам a_i (i=1, 2,…, n). Останется смасштабировать его делением на b_n+1,n+1, так как последний по договоренности равен 1. Его первые n составляющих и образуют искомый вектор решения.

Всю описанную процедуру рекомендуют повторить от 3 до 5 раз для повышения точности результата.

К решению систем линейных алгебраических уравнений приводятся многие задачи численного анализа.

Известное из курса высшей алгебры правило Крамера для решения систем линейных алгебраических уравнений практически невыгодно, так как требует слишком большого количества арифметических операций и записей. Поэтому было предложено много различных способов, более пригодных для практики.

Используемые практически методы решения систем линейных алгебраических уравнений можно разделить на две большие группы: так называемые точные методы и методы последовательных приближений. Точные методы характеризуются тем, что с их помощью принципиально возможно, проделав конечное число операций, получить точные значения неизвестных. При этом, конечно, предполагается, что коэффициенты и правые части системы известны точно, а все вычисления производятся без округлений. Чаще всего они осуществляются в два этапа. На первом этапе преобразуют систему к тому или иному простому виду. На втором этапе решают упрощенную систему и получают значения неизвестных.

Методы последовательных приближений характеризуются тем, что с самого начала задаются какими-то приближенными значениями неизвестных. Из этих приближенных значений тем или иным способом получают новые «улучшенные» приближенные значения. С новыми приближенными значениями поступают точно также и т.д. При выполнении определенных условий можно придти, вообще говоря, после бесконечного числа шагов. Рассмотрим два точных метода: метод ортогонализации и метод сопряженных градиентов.

Метод ортогонализации в случае симметрической матрицы

Пусть дана система

порядка n. Чтобы избежать в дальнейшем путаницы, над векторами поставим черточки. Решение системы будем разыскивать в виде

где – n векторов, удовлетворяющих условиям

Здесь рассматривается обычное скалярное произведение векторов в n-мерном векторном пространстве, т.е. если и , то . Пусть такие векторы найдены. Как это делается, будет показано ниже. Рассмотрим скалярное произведение обеих частей системы (1) с

Используя (2) получим:

или, в силу выбора векторов ,

Итак, для определения коэффициентов получили систему с треугольной матрицей. Определитель этой системы равен

Следовательно, если , то возможно найти и находятся они без труда.

Особенно легко определятся , если матрица А симметрическая. В этом случае, очевидно,

Тогда система для определения примет вид

Метод можно обобщить. Пусть каким-то образом удалось найти систему 2n векторов так, что

Умножая обе части равенства (1) на и используя представление через , как и ранее, получим:

Опять получилась система линейных алгебраических уравнений с треугольной матрицей для определения . Несколько усложнив вычисления можно получить систему диагонального вида. Для этого построим три системы векторов , так что имеют место равенства:

так как при i r

Остановимся подробнее на первом из описанных методов. Рассмотрим случай, когда матрица А симметрическая и положительно определенная. Последнее означает, что для любого вектора квадратичная форма его компонент больше или равна нулю, причем равенство нулю возможно в том и только том случае, если вектор нулевой. Как мы видели ранее, нужно построить систему векторов , удовлетворяющих условиям

Это построение можно осуществить следующим образом. Исходим из какой-то системы линейно независимых векторов , например из системы единичных векторов, направленных по координатным осям:

Далее проводим «ортогонализацию». Принимаем и ищем в виде

Из условия находим:

Условия влекут за собой

Далее поступаем также.

Процесс будет осуществим, так как все . Это же обеспечит нам разрешимость системы для определения коэффициентов . Заметим, что в нашем случае это будет процесс настоящей ортогонализации, если в пространстве векторов ввести новое скалярное произведение при помощи соотношения

Нетрудно проверить, что введенное таким способом скалярное произведение будет удовлетворять всем требованиям, которые к нему предъявляются.

При решении системы n уравнений по настоящей схеме требуется произвести

операций умножения и деления.

Метод ортогонализации в случае несимметрической матрицы

В случае несимметрической матрицы процесс ортогонализации проводится точно также. Пусть векторы уже построены. Тогда ищется в виде

Коэффициенты определяются из системы

Система в случае несимметрической матрицы будет треугольной.

Аналогично строится система «биортогональных» векторов, т.е. система 2n векторов, удовлетворяющих условию (12). При этом – n произвольных линейно независимых векторов, а векторы строятся последовательно в виде

Коэффициенты находятся из системы

Также поступаем, отыскивая коэффициенты и , при построении систем векторов (14) и (15), удовлетворяющих условиям (16).

При этом получим две системы:

из которых и определяем и .

Остановимся еще на одном методе ортогонализации. Будем рассматривать строки матрицы А как векторы:

Ортонормируем эту систему векторов. Первое уравнение системы делим на . При этом получим

Второе уравнение системы заменится на

Аналогично поступаем дальше. Уравнение с номером i примет вид

Процесс будет осуществим, если система уравнений линейно независима. В результате мы придем к новой системе , где матрица С будет ортогональной, т.е. обладает свойством СС=I.

Таким образом, решение системы можно записать в виде

Практически, вследствие ошибок округления, СС будет отлична от единичной матрицы и может оказаться целесообразным произвести несколько итераций для системы .