Метод прогонки в mathcad

Необходимо решить СЛАУ, у которой матрица коэффициентов имеет трехдиагональный вид, методом правой прогонки. Все результаты численных экспериментов свести в таблицу.

Сделать выводы. Оформить отчет по лабораторной работе.

3.4 Порядок выполнения работы на компьютере.

Войти в MathCAD, для этого нужно набрать:

Имя пользователя: Vmstudent

После входа в систему запустить MathCAD 2000 Professional.

Порядок выполнения работы.

Зададим элементы трех диагоналей матрицы acb согласно варианту

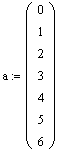
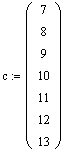
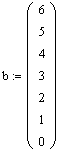
Найдем число элементов в главной диагонали (оно совпадает с числом уравнений в системе) и определим счетчики столбцов с трок

Рассчитаем значения всех членов матрицы acb

Проверим правильность получения матрицы acb (должно быть только три диагонали)

Зададим столбец свободных членов согласно варианту

Проверка условия диагонального преобладания для полученной матрицы acb (если kn-1 = 0, то условие выполняется )

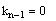
Рассчитаем значения коэффициентов a

Рассчитаем значения коэффициентов b

Рассчитаем значение последнего неизвестного системы уравнений

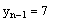
Зададим счетчик для обратного хода

Рассчитаем найдем все оставшиеся неизвестные системы уравнений

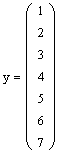
3.5 Содержание отчета.

1.Отчет должен содержать матрицу abc, а также столбец свободных членов.

2.Условие устойчивости метода прогонки.

3.Формулы для расчета коэффициентов 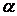и .

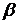4.Матрицы коэффициентов 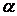и .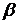

5.Формулу расчета последнего неизвестного СЛАУ.

6.Формулу расчета оставшихся неизвестных СЛАУ неизвестных.

7.Матрицу решения СЛАУ.

3.6. Контрольные вопросы.

• АлтГТУ 419
• АлтГУ 113
• АмПГУ 296
• АГТУ 266
• БИТТУ 794
• БГТУ «Военмех» 1191
• БГМУ 172
• БГТУ 602
• БГУ 153
• БГУИР 391
• БелГУТ 4908
• БГЭУ 962
• БНТУ 1070
• БТЭУ ПК 689
• БрГУ 179
• ВНТУ 119
• ВГУЭС 426
• ВлГУ 645
• ВМедА 611
• ВолгГТУ 235
• ВНУ им. Даля 166
• ВЗФЭИ 245
• ВятГСХА 101
• ВятГГУ 139
• ВятГУ 559
• ГГДСК 171
• ГомГМК 501
• ГГМУ 1967
• ГГТУ им. Сухого 4467
• ГГУ им. Скорины 1590
• ГМА им. Макарова 300
• ДГПУ 159
• ДальГАУ 279
• ДВГГУ 134
• ДВГМУ 409
• ДВГТУ 936
• ДВГУПС 305
• ДВФУ 949
• ДонГТУ 497
• ДИТМ МНТУ 109
• ИвГМА 488
• ИГХТУ 130
• ИжГТУ 143
• КемГППК 171
• КемГУ 507
• КГМТУ 269
• КировАТ 147
• КГКСЭП 407
• КГТА им. Дегтярева 174
• КнАГТУ 2909
• КрасГАУ 370
• КрасГМУ 630
• КГПУ им. Астафьева 133
• КГТУ (СФУ) 567
• КГТЭИ (СФУ) 112
• КПК №2 177
• КубГТУ 139
• КубГУ 107
• КузГПА 182
• КузГТУ 789
• МГТУ им. Носова 367
• МГЭУ им. Сахарова 232
• МГЭК 249
• МГПУ 165
• МАИ 144
• МАДИ 151
• МГИУ 1179
• МГОУ 121
• МГСУ 330
• МГУ 273
• МГУКИ 101
• МГУПИ 225
• МГУПС (МИИТ) 636
• МГУТУ 122
• МТУСИ 179
• ХАИ 656
• ТПУ 454
• НИУ МЭИ 641
• НМСУ «Горный» 1701
• ХПИ 1534
• НТУУ «КПИ» 212
• НУК им. Макарова 542
• НВ 777
• НГАВТ 362
• НГАУ 411
• НГАСУ 817
• НГМУ 665
• НГПУ 214
• НГТУ 4610
• НГУ 1992
• НГУЭУ 499
• НИИ 201
• ОмГТУ 301
• ОмГУПС 230
• СПбПК №4 115
• ПГУПС 2489
• ПГПУ им. Короленко 296
• ПНТУ им. Кондратюка 119
• РАНХиГС 186
• РОАТ МИИТ 608
• РТА 243
• РГГМУ 118
• РГПУ им. Герцена 124
• РГППУ 142
• РГСУ 162
• «МАТИ» — РГТУ 121
• РГУНиГ 260
• РЭУ им. Плеханова 122
• РГАТУ им. Соловьёва 219
• РязГМУ 125
• РГРТУ 666
• СамГТУ 130
• СПбГАСУ 318
• ИНЖЭКОН 328
• СПбГИПСР 136
• СПбГЛТУ им. Кирова 227
• СПбГМТУ 143
• СПбГПМУ 147
• СПбГПУ 1598
• СПбГТИ (ТУ) 292
• СПбГТУРП 235
• СПбГУ 582
• ГУАП 524
• СПбГУНиПТ 291
• СПбГУПТД 438
• СПбГУСЭ 226
• СПбГУТ 193
• СПГУТД 151
• СПбГУЭФ 145
• СПбГЭТУ «ЛЭТИ» 380
• ПИМаш 247
• НИУ ИТМО 531
• СГТУ им. Гагарина 114
• СахГУ 278
• СЗТУ 484
• СибАГС 249
• СибГАУ 462
• СибГИУ 1655
• СибГТУ 946
• СГУПС 1513
• СибГУТИ 2083
• СибУПК 377
• СФУ 2423
• СНАУ 567
• СумГУ 768
• ТРТУ 149
• ТОГУ 551
• ТГЭУ 325
• ТГУ (Томск) 276
• ТГПУ 181
• ТулГУ 553
• УкрГАЖТ 234
• УлГТУ 536
• УИПКПРО 123
• УрГПУ 195
• УГТУ-УПИ 758
• УГНТУ 570
• УГТУ 134
• ХГАЭП 138
• ХГАФК 110
• ХНАГХ 407
• ХНУВД 512
• ХНУ им. Каразина 305
• ХНУРЭ 324
• ХНЭУ 495
• ЦПУ 157
• ЧитГУ 220
• ЮУрГУ 306

Полный список ВУЗов

Чтобы распечатать файл, скачайте его (в формате Word).

БлогNot. Mathcad: решение краевой задачи для дифференциального уравнения 2 порядка

Mathcad: решение краевой задачи для дифференциального уравнения 2 порядка

Краевая задача — это такое дифференциальное уравнение (или даже система дифференциальных уравнений) с заданными линейными соотношениями между значениями искомых функций на начале и конце заданного интервала.

Частые применения дифуров (обыкновенных дифференциальных уравнений, ОДУ) – решение задач вариационного исчисления, оптимального управления, механики жидкости и газа, баллистики, теории упругости и т.д.

Например, очень распространена на практике (и достаточно универсальна) такая постановка: для дифференциального уравнения второго порядка, имеющего вид

u” + p(t)*u’ + g(t)*u = f(t) , t принадлежит интервалу [a,b]

поставлена краевая задача

Здесь u(t) – искомое решение, A , B – заданные краевые условия, определяющие значения искомой функции на концах интервала, p(t) , g(t) , f(t) – заданные функции коэффициентов, а штрихами, как обычно, обозначаем производные.

Если не вдаваться глубоко в теорию (она есть, например, тут, правда, обозначения другие), то такие задачи решаются методом конечных разностей, суть которого вот в чём:

1. Область непрерывного изменения аргумента t (интервал [a,b] ) заменяется дискретным множеством точек (узлов). Количество этих узлов мы будем обозначать m , так что у нас выйдет дискретный аргумент t_i = a + τ*i , i=0,1. m , τ=(b-a)/m .

2. Искомая функция u(t) непрерывного аргумента t приближённо заменяется функцией дискретного аргумента t_i на заданной сетке (а производные можно заменить конечными разностями, просто по определению производной). Такая функция называется сеточной.

3. Исходное дифференциальное уравнение заменяется уравнением относительно сеточной функции. Это и есть разностная аппроксимация.

Решение уравнения в нашей постановке сводится к решению СЛАУ с трёхдиагональной матрицей, размерность которой будет (m+1)*(m+1) , а все ненулевые элементы сосредоточатся на главной диагонали и двух прилегающих к ней диагоналях.

Было бы нерационально решать такую систему "в лоб", для неё есть экономичный метод прогонки. Ну а мы реализуем его и конечно-разностный метод в целом при помощи MathCAD.

В тестовых целях возьмём на просторах инета вот такую задачу, для которой известно решение:

Введём в документ MathCAD все исходные данные задачи в виде переменных:

Это позволит вам, задав свои данные, решить другую задачу.

Реализуем метод прогонки решения краевой задачи для ОДУ 2 порядка, написав подпрограмму-функцию Progonka . Для простоты она будет пользоваться описанными выше переменными, а не получать кучу параметров.

Как и при решении задачи Коши, возвращаем матрицу из 2 столбцов, первый из которых – значения t_i в узлах сетки, второй – вычисленные значения y_i дискретной функции.

В учебных целях определим функции u(t) – точное решение задачи и Solution – формирование таблицы значений функции точного решения в тех же точках, в которых мы искали решение численным методом.

Останется вызвать обе функции и сравнить, что получилось, взяв норму разности векторов точного и приближённого решения. Оба этих действия на скрине:

По малому значению погрешности видно, что прогонка работает хорошо, при увеличении значения m вдвое погрешность уменьшается для тестовой задачи более, чем вдвое, вывод о порядке аппроксимации метода сделайте сами 🙂

В прилагаемом документе Mathcad есть также график, сюда не вывожу.

Решение краевой задачи для дифференциального уравнения 2 порядка, документ MathCAD 14/15 (.xmcd) в архиве .zip (36 Кб)

Решение краевой задачи стандартной функцией sbval можно попробовать тут

15.11.2014, 16:16; рейтинг: 21797

Неявная схема Эйлера

Алгоритм прогонки

Приведем в данном разделе описание чрезвычайно популярного алгоритма реализации неявных разностных схем, который называется методом прогонки. Этот алгоритм имел историческое значение для становления технологий расчетов уравнений в частных производных, и мы просто не можем не упомянуть о нем в этой книге.

Сразу оговоримся, что его применение для решения уравнений в частных производных в среде Mathcad может быть оправдано, только если Вы работаете с очень частыми сетками, которые приводят к системам разностных уравнений большой размерности и, соответственно, очень долгому времени вычислений.

Основным вычислительным ядром программы, реализующей на Mathcad неявную разностную схему, было решение (на каждом временном слое) системы линейных алгебраических уравнений, задаваемых матрицей А. Заметим, что эта матрица, как говорят, имеет диагональное преобладание, а точнее, является трехдиагональной (рис. 13.13). Все ее элементы, кроме элементов на главной диагонали и двух соседних диагоналях, равны нулю. С точки зрения оптимизации быстродействия алгоритма, применение встроенной функции isolve является весьма расточительным, поскольку основной объем арифметических операций, выполняемых компьютером (а он составляет, как нетрудно убедиться величину порядка M 2 ), сводится к непроизводительному перемножению нулей.

Для отыскания решения линейных систем алгебраических уравнений имеется чрезвычайно эффективный алгоритм, называемый прогонкой, который позволяет снизить число арифметических операций на целый порядок, т. е. до значения порядка м. Это означает, что при использовании пространственных сеток с 1000 узлами выигрыш во времени вычислений составит величину порядка 10 3 ! Реализация данного алгоритма приведена в листинге 13.3, который является продолжением листинга 13.2, используя определенные в нем коэффициенты матрицы А, а также начальное условие.

Листинг 13.3. Алгоритм прогонки (продолжена листинга 13.2):

Программа листинга 13.3 осуществляет пересчет одного шага по времени, т. е. заменяет содержимое столбца и с предыдущего временного слоя вычисленными значениями неизвестной функции со следующего слоя. Первые пять строк листинга 13.3 представляют так называемый обратный ход прогонки, а последние две строки – ее прямой ход. Заинтересовавшемуся читателю предлагается самому оформить представленный алгоритм прогонки в виде программы решения разностных уравнений для вычисления произвольного временного слоя по примеру листингов 13.1 и 13.2. Заметим, что описание этого знаменитого алгоритма можно отыскать практически в любом современном учебнике по численным методам.

Рис. 13.13. Матрица системы линейных разностных уравнений для неявной схемы (листинг 13.2 для М=10)