Модель черного ящика на примере школы

Модель «черного ящика», примеры которой будут приведены далее, представляет собой иллюстрацию объекта, для которого заданы выход и вход. При этом его содержимое неизвестно. Рассмотрим далее, как построить модель «черного ящика».

Первый этап

В качестве исходного действия, необходимого для составления модели абсолютно любой системы, выступает отделение объекта от окружающей его среды. Эта простейшая операция отражает два важнейших свойства: обособленность и целостность предмета. Объектом исследования является некий объект, содержимое которого неизвестно.

Взаимодействия со средой

Любая модель состава системы не является полностью изолированной. Она поддерживает с окружающей средой определенные связи. С их помощью происходит взаимное воздействие объекта и условий, в которых он находится. Соответственно, при выстраивании модели «черного ящика» на следующем этапе связи изображаются стрелками и описываются словами. Те, которые направлены в среду, являются выходами. Соответственно, обратные стрелки будут входами.

На этом уровне представления системы исследователь имеет дело с декларативной моделью. То есть выходы и входы определяются по шкале наименований. Как правило, достаточно такого отображения. Однако в ряде случаев необходимо дать количественное описание некоторых либо всех выходов и входов.

Множества

Они задаются для того, чтобы модель «черного ящика» была максимально формализована. В результате исследователь приходит к заданию 2 множеств Y и Х выходных и входных переменных. При этом никакие отношения между ними на данном этапе не фиксируются. В противном случае получится модель прозрачного, а не «черного ящика». Так, для телевизора множеством Х могут являться предельные диапазоны сетевого напряжения и радиоволн трансляции.

Модель «черного ящика»: системный анализ

На заключительном этапе исследуются и отражаются изменения объекта. К примеру, они могут происходить в течение определенного времени. То есть исследователь иллюстрирует состояние объекта в динамике. Описание модели «черного ящика» должно показывать соответствия, во-первых, компонентов множества Х вероятных величин входных параметров и элементов упорядоченного Т-множества временных отрезков. Кроме этого, должно быть отображено аналогичное соотношение для выходных показателей.

Специфика

Ключевым достоинством рассматриваемого объекта выступает его простота. Между тем, она во многих случаях весьма обманчива. Достаточно часто перечисление выходов и входов представляет собой довольно сложную задачу. Если рассмотреть автомобиль как модель типа «черный ящик», то этот вывод подтвердится. Мощность множеств при исследовании этого объекта превысит два десятка. При этом перечень параметров будет далеко не полным.

Такая множественность выходов и входов обуславливается неограниченностью вариантов взаимодействия рассматриваемого предмета со средой.

Нюансы

Структурная модель системы применяется в тех случаях, когда нужно иллюстрировать сложный объект, в котором содержится несколько элементов. В простейших ситуациях в ней присутствует набор компонентов. Все они включены в сам объект. В этих случаях применяется понятие «модель состава системы».

Между тем, существует ряд вопросов, которые нельзя решить с ее помощью. В частности, чтобы собрать велосипед, недостаточно наличия ящика со всеми его элементами. Нужно знать, как правильно их соединить друг с другом. Очевидно, что только лишь модель состава системы в этом случае не поможет. Более того, в ряде случаев необходимо установить между компонентами определенные связи. Их характер показывает структурная схема. Она дает возможность решить больше задач. Структурная схема отвечает на вопросы: «Что входит в объект и каковы связи между его элементами?»

Пояснения

Особое значение для человека имеют наглядные визуальные образы. Используемое на практике определение системы не характеризует ее внутреннее устройство. Это позволяет выделить ее из среды. При этом она будет изображаться как модель «черного ящика» – целостный и относительно обособленный предмет. Достигнутая цель представляет собой заранее запланированные изменения в среде, определенные продукты работы объекта, предназначенные для потребления вне его. Другими словами, модель черного ящика устанавливает определенные связи и влияет на внешние условия. Как выше было сказано, они являются выходами.

Вместе с этим система выступает как средство. Поэтому необходимы возможности для ее применения, воздействия на нее. Соответственно, устанавливаются связи из среды в объект – входы. Использование модели «черный ящик» позволяет изучить только взаимодействие предмета и среды. В ней отображаются только входные и выходные параметры. При этом в ней даже отсутствуют границы между средой и объектом (стенки ящика). Они только подразумеваются, считаются существующими.

Модель «черного ящика»: примеры

Как говорилось выше, иногда достаточно словесного содержательного отображения выходов и входов. В этом случае модель черного ящика будет являться их перечнем. Так, для телевизора отображение связей будет следующим:

1. Входы – кабель питания, антенна, элементы настройки и управления.
2. Выходы – экран и динамики.

В других ситуациях может потребоваться количественное отображение связей.

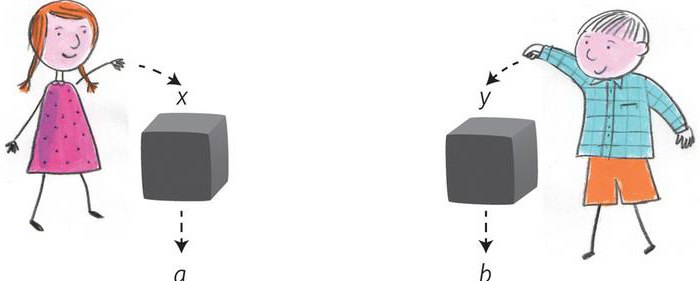
Возьмем другую систему – наручные часы. Следует принять во внимание, что выходы направлены на конкретизацию цели. Соответственно, в качестве одного из них можно зафиксировать показание времени в какой-либо произвольный момент. Далее следует учесть, что выраженная цель относится в целом ко всем часам, а не только к взятым наручным. Для их дифференциации можно внести следующее добавление – удобство ношения на запястье. Оно будет выступать в качестве входа. С этим добавлением возникает необходимость браслета или ремешка. С ним, в свою очередь, появляется обязательность удовлетворения правилам гигиены (выход), поскольку не каждое крепление допустимо на руке. Затем, если представить условия, в которых эксплуатируются часы, можно ввести еще несколько параметров: пылевлагонепроницаемость, прочность. Дополнительно можно применить еще два выхода. Ими будут точность, необходимая в повседневной жизни, а также доступность информации на циферблате для прочтения при беглом взгляде. В процессе исследования можно добавить еще несколько требований к часам. Например, вводятся такие выходы, как соответствие моде, соотношение цены с покупательской способностью потребителя.

Вполне очевидно, что этот перечень можно продолжать. В него допустимо включить требование о прочтении информации с циферблата в темноте. Реализация его приведет к значительному изменению конструкции. В ней могут предусматриваться, например, разные варианты самосвечения, считывания на ощупь, подсветки, подачи сигналов и пр.

Характеристика хозяйствующего общества

Рассмотрим специфику построения модели на примере предприятия. Стоит сразу сказать, что ее создание базируется на выделении из бесконечного множества взаимодействий такого их набора, который адекватно отражал бы цель исследования. Безусловно, такую модель не следует сводить к моносистеме. То есть к такому объекту, у которого есть только по одному входу и выходу.

Модель «черный ящик» рассматривает организацию как систему связей предприятия с окружающей средой. При анализе для обоснования достаточного и необходимого набора параметров множеств выходов и входов широко применяются приемы математической статистики. Зачастую к процессу привлекаются и опытные эксперты.

Что касается отношений компании и окружающей среды, то здесь следует дать несколько пояснений. В первую очередь для ведения производственной деятельности необходим капитал. Он может быть представлен в форме заемных средств или собственных акций фирмы. За счет ликвидных активов предприятие получает возможность задействовать в процессе производственные факторы. Ими, как известно, являются материалы, оборудование и прочие ресурсы, которые преобразуются в готовую продукцию.

Еще одна связь с окружающей средой выражена в процессе сбыта изделий. Реализация продукции дает предприятию средства, которые, в свою очередь, направляются на погашение задолженностей, оплату труда и так далее. На заемные средства начисляются проценты. Они уплачиваются кредитной организации. Кроме этого, компания отчисляет обязательные платежи в бюджет. Вместе с этим, государство предоставляет фирме дотации.

Практическое значение

Зачастую модель «черного ящика» является не только весьма полезной, но и единственно доступной для использования при исследовании. К примеру, при анализе психических процессов в организме человека либо влияния медикаментов на пациента специалисты могут вмешиваться во внутренние процессы только через входы. Соответственно, выводы делаются на основании исследования выходов.

В целом данное положение относится к таким наблюдениям, в результате которых необходимо получить сведения о системе в привычных для нее условиях, в обстановке, где нужно особенно заботиться о том, чтобы процесс измерения оказывал минимальное на нее воздействие.

Применение такого «непрозрачного» объекта обуславливается также тем, что у исследователя нет информации о внутреннем его устройстве. В частности, неизвестно, как устроен электрон. Но установлено, как он взаимодействует с магнитным, гравитационным, электрическим полями. Такая характеристика и есть описание электрона по принципу модели «черного ящика».

Дополнительно

Необходимо отметить еще одно важное явление. Рассматриваемая модель уже структурирована. В ней известно, относится ли связь к категории выходов или входов. Между тем, на начальных этапах исследования и эти сведения могут отсутствовать. Исследователь имеет возможность выделить определенную связь объекта со средой, наблюдать и измерять какой-либо параметр, по которому она характеризуется. Однако при этом не будет достаточно оснований безусловно установить ее направленность.

В таких ситуациях целесообразно исследовать два конкурирующих черных ящика. В одном связь будет рассматриваться как вход, в другом, соответственно, как выход. В качестве примера может выступать исследование процессов, для которых не установлено, какой является следствием, а какой – причиной, или вообще относится ли их связь к категории причинно-следственных.

Критерии выбора

Множественность выходов и входов обуславливается неограниченным количеством взаимодействий между объектом и средой. При выстраивании модели выбирается определенный набор связей, которые будут включены в перечень выходов и входов. В качестве критерия в таком случае выступает целевое назначение объекта, существенность взаимодействия относительно цели.

Соответственно, выбор делается следующим образом. Все, что существенно, включается в модель, а все, что таковым не является, – исключается из нее. Однако именно на этом этапе могут быть допущены ошибки. Тот факт, что в модели не учитывается определенный набор связей, не делает их нереальными. Они в любом случае существуют и действуют вне зависимости от воли исследователя, делающего выбор.

Зачастую оказывается, что представлявшиеся ранее неизвестными или несущественными условия на самом деле очень важны и должны быть учтены. Особое значение данный момент имеет при определении цели системы. При установлении выходов объекта основную задачу приходится дополнять вспомогательными проблемами. Следует подчеркнуть, что исполнения только ключевой цели будет недостаточно. При этом нереализация дополнительных задач может сделать в одних случаях ненужным, в других – опасным – решение основной проблемы.

На данный момент необходимо обратить особое внимание, поскольку на практике зачастую обнаруживается непонимание, незнание либо недооценка значения этого положения. В действительности же оно выступает в качестве одной из центральных идей системологии.

Заключение

Модель непрозрачного (черного) ящика считается самой простой в системологии. Между тем, при ее создании зачастую возникают разнообразные сложности. Они обуславливаются главным образом многообразием возможных вариантов установления связей между объектом и средой, в которой он расположен. При использовании модели необходимо учитывать разнообразные факторы, четко определять конечные и дополнительные цели. Исполнение последних зачастую крайне важно для получения запланированных результатов наблюдения.

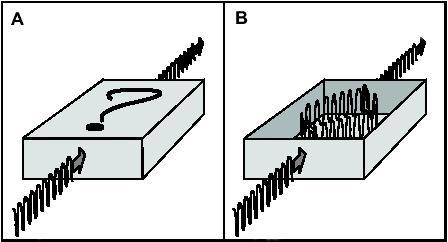
“Черный ящик” (ЧЯ)– объект, у которого исследователю известны вход и выход, а внутреннее строение неизвестно. Название образно подчеркивает полное отсутствие сведений о внутреннем содержимом “ящика”.

Укажем основные этапы построения модели в виде ЧЯ

1. Первым действием, которое необходимо выполнить при составлении модели любой системы – отделение объекта исследования от окружающей среды. Простейшим наглядным образом реализации данной операции может служить представление системы в виде непрозрачного “ящика”, выделенного из окружающей среды. Уже эта, максимально простая, модель по-своему отражает два важных свойства системы: целостность и обособленность от среды.

2. Любая система не совсем изолирована от окружающей среды, а поддерживает с ней определенные связи, посредством которых система и среда как-то воздействуют друг на друга. Поэтому следующим (вторым) этапом моделирования может быть изображение этих связей в виде стрелок, направленных из системы в среду – выходы, и из среды к системе – входы и содержательного словесного описания входов и выходов.

При таком уровне представления системы мы имеем дело с её декларативной моделью, т.к. входы и выходы определены на шкале наименований. Во многих случаях достаточно такой модели, однако часто бывает необходимым количественно описать некоторые или все входы и выходы системы.

3.Пытаясь максимально формализовать модель ЧЯ, мы приходим к заданию двух множеств Х и Y входных и выходных переменных (третий этап), но никаких других отношений между этими множествами фиксировать не будем (иначе это уже будет не “черный”, а “прозрачный” ящик). Например, для модели телевизора в качестве множества X можно указать допустимые диапазоны напряжения в сети и радиоволн телетрансляции.

4.Четвёртым этапом развития модели является описание изменений, происходящих в системе, например, с течением времени, т.е. описание её динамики. На уровне ЧЯ эта модель должна отображать соответствие во-первых, между элементами множества Х возможных значений входных параметров и элементами упорядоченного множества Т моментов времени в виде отображения Т ® Х, а во-вторых – между элементами множества Y возможных значений выходных параметров и моментами времени в виде отображения Т ® Y. Таким образом, имеем модель в виде совокупности двух процессов <x(t), y(t)>.

Главное достоинство модели “черный ящик” – её простота, поскольку описание и исследование входов и выходов обычно намного проще, чем внутреннего строения объекта.

Однако необходимо подчеркнуть, что эта простота обманчива. Весьма часто перечисление входов и выходов реальной системы представляет собой сложную задачу. Например, пытаясь перечислить все более или менее важные входы и выходы системы “автомобиль” мы очень быстро поймем это, поскольку мощность множеств Х и Y как-то легко перевалит за два десятка, а список параметров все еще не полон. Главной причиной такой множественности входов и выходов является неограниченность числа способов, которыми любой объект взаимодействует со средой.

Структурная модель используется, когда необходимо описать строения сложного объекта, состоящего из нескольких частей. В простейшем случае эта модель включает в себя перечень элементов, входящих в объект и тогда используется термин “модель состава”. Примеры моделей состава для некоторых систем приведены в таблице 5.3.

Однако очевидно, что есть вопросы, решить которые с помощью модели состава нельзя. Чтобы получить велосипед, недостаточно иметь ящик со всеми его деталями (элементным составом). Необходимо еще правильно соединить все детали между собой, или установить между элементами определенные связи – отношения. Такая, более сложная модель, кроме состава показывает характер связей между частями объекта. Обычно именно такая модель и называется структурной.

Таким образом, структурная модель объекта является ответом на вопрос “из чего состоит объект и как связаны эти части?”

Таблица 5.3
Примеры моделей состава
№ п/п	Система	Подсистемы	Элементы
Система телевидения	Передающая подсистема	Центральная телестудия
Антенно-передающий центр
Канал связи	Среда распространения радиоволн
Спутники-ретрансляторы
Приемная подсистема	Местные телецентры
Телевизоры потребителей
Семья	Члены семьи	Муж
Жена
Предки
Потомки
Другие родственники
Имущество семьи	Общее жилье и хозяйство
Личная собственность членов семьи

Пример 5.4.Рассмотрим объект “часы вообще”, структурная модель которого приведена на рис 5.1. Считаем, что в его состав входят три элемента:

– датчик времени (процесс, течение которого изображает ход времени – раскручивание пружины, качание маятника, течение струйки песка и т.п.);

– индикатор времени (устройство, преобразующее текущее состояние датчика в сигнал времени для пользователя – две стрелки, цифровой дисплей на жидких кристаллах, уровень песка в сосуде и пр.);

– эталон времени (механизм, определяющий истинное время – сигнал “точного времени” по радио, атомные часы службы точного времени, положение звезд на небосводе и т.д.).

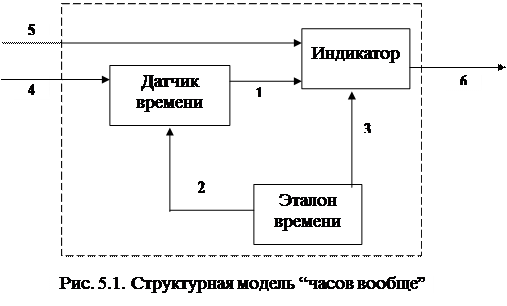На рис. 5.1 обозначены цифрами 1– 3 связи межу элементами системы. Кроме того, на нём обозначены входы: 4 – поступление энергии извне, 5 – регулировка индикатора и выход: 6 – показания часов.

Для представления структурных моделей пришлось абстрагироваться от содержательной стороны структур, оставив только общее для каждой системы. В результате получилась конструкция, в которой обозначается только наличие элементов и связей между ними. Такая схема называется графом и является наиболее наглядной и компактной формой представления структурной модели.

Граф – конструкция, включающая в себя некоторое множество V (обычно конечное) и определенное на нем отношение E. Геометрическим образом графа является фигура, состоящая из точек (вершин), соединенных линиями (ребрами). Точки соответствуют элементам объекта, ребра – имеющимся связям. Направленные связи снабжаются стрелками и называются ориентированными ребрами или дугами.

Помимо графов используются другие изобразительные средства представления структурной модели, например, матрицы или таблицы.

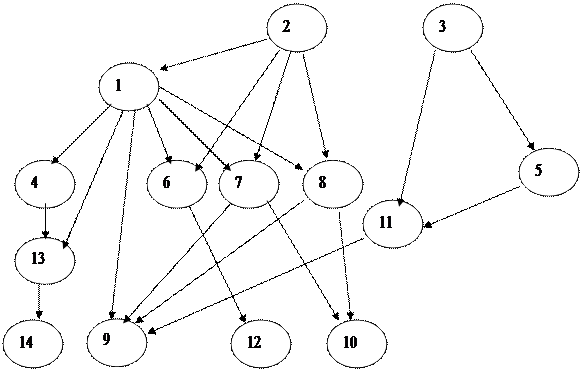Рис. 5.2. Граф трофической структуры системы А

Пример 5.5. На рис. 5.2 дана трофическая структура (структура питания) некоторой экосистемы. Трофическую структуру типа "хищники и жертвы" образует отношение R = <x поедает y>, определённое на множестве пар элементов множества А. Здесь экосистема состоит из следующих обитателей A = <1 – человек, 2 – тигр, 3 – коршун, 4 – щука, 5 – змея, 6 – кабан, 7 – баран, 8 – газель, 9 – пшеница, 10 – клевер, 11 – полевка, 12 – желудь, 13 – карась, 14 – водоросль>.

Функциональная модель. Следующий шаг в исследовании объектов произвольной природы после определения его состава и связей состоит в том, чтобы понять и описать, как объект “работает”, что происходит в самом объекте и окружающей его среде в ходе реализации поставленной цели. Соответствующие модели должны отражать поведение объекта при меняющихся условиях (в частности – с течением времени), описывать последовательность каких-то этапов, операций, действий, причинно-следственные отношения, т. е. описывать процесс функционирования объекта. Такая модель называется функциональной. Она имеет вид математических соотношений, отражающих те законы природы и закономерности, согласно которым функционирует объект.

Опишем основные этапы построения функциональной модели.

1. Состояние объекта – это множество его существенных свойств в данный момент времени. Функционирование системы тесным образом связано с её состояниями. Поэтому первым этапом синтеза функциональной модели является выделение множества различных состояний моделируемого объекта, конечного или бесконечного.

2. Далее необходимо выявить связи между различными состояниями системы и определить степени их взаимного влияния. Кроме того, надо отметить степень влияния входных воздействий. Вначале эти связи следует определить хотя бы качественно, т.е. на уровне отношений между соответствующими множествами допустимых значений.

3. В результате экспериментов или теоретических выкладок эти связи должны приобрести вид конкретных математических соотношений в виде уравнений, алгоритмов или иных зависимостей. Этот этап принято называть параметризацией.

4.В своем окончательном виде функциональная модель должна отражать динамку объекта, т.е. отражать процесс изменения состояний системы с течением времени.

Внешне функциональная модель обычно представляет собой систему математических выражений (формул), например, в виде дифференциальных и/или алгебраических уравнений. Но иногда используются модели иной структуры, например, графические – сетевые графики (для представления временной последовательности выполняемых действий), сети Петри (диаграммы причинно-следственных связей), блок-схемы (последовательность шагов реализации инструкций, алгоритма) и т.п. Выбор того или иного типа модели определяется типом протекающих процессов и целью моделирования.

5.5. Классификация по этапам жизненного цикла модели

Понятие жизненного цикла является удобной концепцией описания развития любой системы от её рождения до гибели. В ходе решения поставленной задачи (реализации цели моделирования) математическая модель претерпевает определенные изменения, поэтому понятие жизненного цикла подходит и для описания этих фаз (см. рис. 4.1).

1. Выработка концепции или построение концептуальной модели. Концептуальная модель – сформулированный в терминах прикладных дисциплин перечень вопросов, интересующих исследователя, а также совокупность гипотез и допущений относительно свойств и поведения объекта моделирования, его взаимодействии с окружающей средой. Эти гипотезы должны быть достаточно правдоподобны в том смысле, что для их обоснования могут быть приведены какие-то теоретические доводы или результаты экспериментов из набора начальных знаний об объекте.

На основании принятых гипотез определяется перечень и характер параметров, описывающих объект, а также перечень законов, согласно которым происходит изменение и взаимосвязь этих параметров.

Пример 5.6.Имеем словесную постановку задачи.

Разработать математическую модель, позволяющую описать полёт баскетбольного мяча, брошенного в корзину. Модель должна позволять вычислять положение мяча в любой момент времени при различных начальных условиях.

Примем следующие допущения:

– объектом моделирования считается баскетбольный мяч массы m радиуса R;

– мяч считать материальной точкой заданной массы m, положение которой совпадает с центром масс мяча;

– движение мяча описывается в соответствии с законами классической механики;

– движение происходит в поле сил тяжести с постоянным ускорением свободного падения;

– движение происходит в одной плоскости, перпендикулярной поверхности Земли и проходящей через точку броска и центр корзины;

– пренебрегаем сопротивлением воздуха и возмущениями, вызванными собственным вращением мяча вокруг центра масс.

Рассмотрим основные доводы в пользу принятых гипотез.

1) Первая из перечисленных гипотез особенно важна, т.к. она выделяет объект моделирования. Как вариант в качестве объекта можно было считать систему «Игрок – мяч – кольцо». Требуемая для описания подобной системы модель будет уже намного сложнее, т.к. игрок представляет собой сложную биомеханическую систему и его моделирование – далеко не тривиальная задача. Выбор в качестве объекта только мяча вытекает из самой постановки задачи. Влияние игрока можно учесть через начальные параметры броска

2) Гипотеза о том, что мяч можно считать материальной точкой, широко применяется для исследования тел в механике. В данном случае она оправдана по следующим причинам:

– мяч является симметричным телом

– его радиус мал по сравнению с характерным расстоянием перемещения.

3) Применимость законов классической механики обусловлена малой скоростью движения по сравнению со скоростью света.

4) Гипотеза о постоянстве ускорения обоснована малым перемещением мяча и небольшой высотой полёта. Если бы эти условия не соблюдались, пришлось бы учитывать изменение ускорения в зависимости от широты места и высоты полёта.

5) При выдвижении гипотезы о плоском движении мяча мы исходили из того, что для человека «наведение на цель» в горизонтальной плоскости намного проще, чем в вертикальной. Поэтому можно считать, что направление на центр корзины при броске выдержано точно, т.е. плоскость движения мяча известна, и нас интересует более сложная процедура расчёта расстояния, на котором мяч опустится до уровня кольца.

6) Гипотеза об отсутствии сопротивления воздуха наименее обоснована. При движении тел в жидкости и газе сопротивление усиливается с ростом скорости движения. Учитывая невысокие скорости движения мяча, его правильную обтекаемую форму и малые дальности бросков, данная гипотеза может быть принята в качестве первого приближения (дальше можно скорректировать).

В соответствии с изложенными гипотезами в качестве параметров движения мяча можно использовать координаты (x, y) и проекции скорости (v_x, v_y) центра масс мяча.

2. Переложение на язык математических соотношений цели моделирования, которая обычно задается в словесном (вербальном, неформализованном) виде и запаса исходных знаний об объекте. В результате такого действия получается модель описания – формализованная запись содержания поставленной задачи в виде совокупности математических соотношений, которые связывают между собой исходные данные и результаты счета.

Пример 5.7. Рассмотрим следующую “школьную” задачу. Лошадь и мул несли по несколько мешков с мукой. Лошадь жаловалась на тяжёлую поклажу. «Что ты жалуешься? – отвечал ей мул (см. далее таблица 5.4).

Таблица 5.4.
Исходные знания	Ведь если я возьму у тебя один мешок, моя ноша станет вдвое тяжелее твоей. А вот если бы ты сняла с моей спины один мешок, твоя поклажа стала бы одинакова с моей.
Цель моделирования	Узнать, сколько же мешков несла лошадь, и сколько нёс мул?

Записав условия задачи в формализованном виде, мы получим математическую модель описания. Обозначим Х и Y – количество мешков на спине лошади и мула, соответственно. Чтобы яснее можно было понять связь между словесным и формализованным описанием, представим процесс формализации в виде таблицы 5.5.

Таблица 5.5.
Словесное описание	Формализованное описание
Поклажа лошади (мешки)	X шт.
Поклажа мула	Y шт.
Если я возьму у тебя один мешок,	X – 1
моя ноша	Y + 1
станет вдвое тяжелее твоей.	Y + 1 = 2 (X – 1)
Если бы ты сняла с моей спины один мешок,	Y – 1
твоя поклажа	X + 1
стала бы одинакова с моей	Y – 1 = X + 1

В результате получаем модель описания в виде системы двух уравнений:

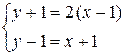. (5.2)

3. Далее строится модель решения – набор математических выражений, указывающих способ получения решения задачи. Важным этапом получения модели решения является составление вычислительной задачи – некоторой стандартной математической задачи, решение которой не требует специальных преобразований, а сводится к набору вычислений. Так, после преобразования системы (5.2) к стандартному виду получим систему уравнений

, (5.3)

которая является вычислительной задачей – решение системы линейных алгебраических уравнений. Запишем способ решения этой системы, например, по формулам правила Крамера:

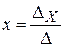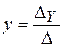; . (5.4)

Это и будет моделью решения.

4.Построение алгоритмической модели – запись решения в виде алгоритма. Ее отличие от модели решения состоит в том, что последняя не обязана обладать всеми свойствами алгоритма: конечность, определённость, результативность, массовость, эффективность. Чаще всего модель решения не обладает свойством конечности.

Для задачи о муле и лошади построим по модели (5.4) следующий алгоритм.

Шаг 1. Вычислим определитель матрицы системы D = 2×(1) – (–1)×(–1) = 1. Он не равен 0, значит, система имеет решение.

Шаг 2. Вычислим определители для каждого неизвестного: D_X = 3 + 2 = 5; D_Y = 4 + 3 = 7.

Шаг 3. Вычисляем каждое неизвестное: ; .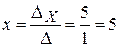

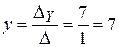Ответ: Мул нёс 7 мешков, а лошадь – 5.

5. Построение программной модели – запись алгоритма в виде программы.

Для решения системы (5.3) можно написать программу, например на языке Pascal. Запишем систему из двух уравнений в общем виде:

Программа, реализующая описанный выше алгоритм, будет иметь вид:

var x,y,A11,A12,A21,A22,b1,b2,Dx,Dy,D : real;

begin readln(A11,A12,b1);

D:=A11*A22-A21*A12;

Dx:=b1*A22-b2*A12;

Dy:=A11*b2-A21*b1;

x:=Dx/D; y:=Dy/D;

readln;

End.

Данная технология составления программной модели применялась в 70-е годы, когда для каждой более или менее типовой задачи писали специальную программу. В наши дни в качестве инструментария ИТ используют мощные вычислительные системы, такие, как например, MathCAD, Excel и др.

Не нашли то, что искали? Воспользуйтесь поиском:

Лучшие изречения: Да какие ж вы математики, если запаролиться нормально не можете. 8546 – | 7400 – или читать все.

91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.

Отключите adBlock!
и обновите страницу (F5)
очень нужно

Урок 2. Информатика 11 класс ФГОС

Конспект урока "Модели систем. Модель черного ящика. Модель состава"

На данном уроке мы познакомимся с такими понятиями как анализ, синтез, системный анализ. Вспомним модель «чёрного ящика» и модель состава.

Система – это целостная и взаимосвязанная совокупность частей, существующая в некоторой среде и обладающая определённым назначением, подчинённая некоторой цели.

Человеческое общество развивается благодаря открытиям, исследованиям, экспериментам и любая система подлежит изучению.

Исследование системы включает в себя два этапа: анализ и синтез.

Анализ системы – это выделение её частей с целью прояснения состава системы.

Как нам уже известно, любая система состоит из подсистем. В свою очередь, любая подсистема состоит так же из нескольких подсистем. Таким образом, мы может разделить систему на самые мелкие объекты.

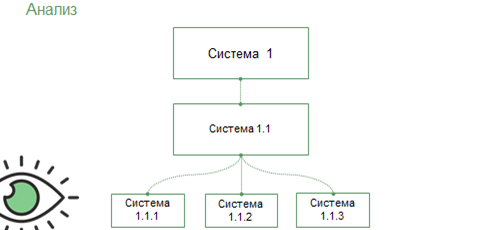
Возникает вопрос: а нужно ли нам это?

На первом этапе необходимо проанализировать систему для определения её состава и цели исследования. Целью исследования системы является получение её модели. Модель – это новый упрощённый объект, который отражает существенные особенности реального объекта, процесса или явления.

Соответственно с помощью модели мы можем получить необходимые нам результаты исследований. Например, узнать, как будет лететь самолёт при большой нагрузке багажом.

Далее необходимо выделить в системе связи между её частями. Например: основные компоненты велосипеда (рама, руль, колеса, педали, сиденье) зависят друг от друга. Качество данной системы – возможность ездить на велосипеде. Ни одна составная часть не обладает этим свойством. Но в свою очередь если собрать их вместе, связать их в одно целое, то появляется такое качество, как возможность ездить на велосипеде.

Состояние и поведение системы в той или иной ситуации можно понять и изучить только при наличии её состава и структуры.

Это был первый этап исследования системы.

Синтез – это мысленное или реальное соединение частей в единое целое. В результате данного этапа создаётся представление о системе, объясняется механизм системного эффекта.

Вывод: системный анализ – это исследование реальных объектов и явлений с точки зрения системного подхода, состоящее из этапов анализа и синтеза.

Любое описание системы отражает ограниченное число её свойств. Это зависит от того, с какой целью мы делаем описание, какие именно качества системы нам нужны.

На этом уроке мы познакомимся с моделью «чёрного ящика».

Есть такое понятие «Система как «чёрный ящик». Оно употребляется в том случае, если человек не знает, как устроена та или иная система «внутри» или эта система не представляет для него интереса. Часто достаточно знать, какие действия можно производить с системой, и какие результаты при этом можно получить.

Вход системы – это воздействие на систему со стороны внешней среды, а выход – это воздействие, которое оказывает система на окружающую среду.

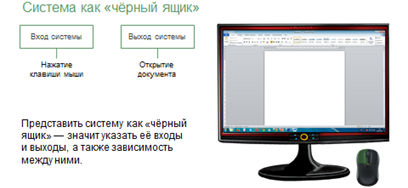
Мы можем понимать, например, что объект на компьютере можно открыть двойным нажатием левой кнопкой мыши на нём. Входом будет нажатие клавиши мыши, а выходом – открытие документа. Но мы не знаем, как это происходит в системном блоке, сам процесс нам не понятен. В таких случаях и применяется понятие «система как «чёрный ящик».

Представить систему как «чёрный ящик» – значит указать её входы и выходы, а также зависимость между ними.

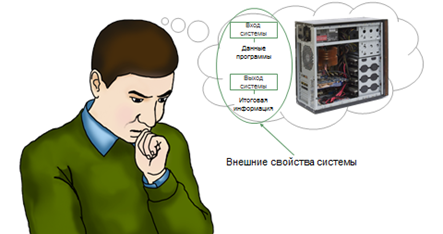
Если описать компьютер как «чёрный ящик», учитывая только входы и выходы системы, то получится, что входом системы являются данные программы, а выходом – итоговая информация.

Вывод: модель «чёрного ящика» представляет систему на уровне описания связей её входов и выходов.

Но в то же время, при решении вопросов, которые касаются внутреннего устройства системы, мы не можем ограничиться лишь моделью «чёрного ящика». Можно сказать, что данные, которые мы получаем при рассмотрении модели «чёрного ящика» по большей части являются лишь внешними свойствами системы.

Поэтому приходится обращаться к модели состава. Модель состава – это своеобразный список элементов системы. В данной системе не рассматриваются связи между её элементами.

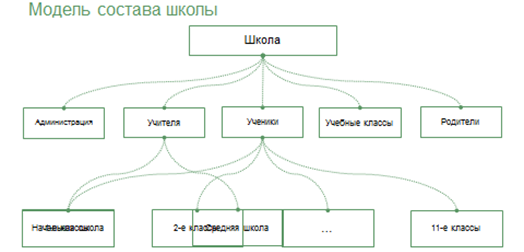
Разберёмся более подробно на модели состава школы.

Любая школа состоит из администрации, учителей, учеников, учебных классов и родителей. На данной схеме мы видим пять составляющих нашей системы. Каждая из них является подсистемой со своим составом. Для этих подсистем можно также построить свои схемы состава. Например, учеников можно разделить по параллелям с первых по одиннадцатые классы. Или же учителей можно разделить на начальную и старшую школы.

Очевидно, что такой модели будет мало, если мы захотим разобраться, как функционирует школа. Но с другой стороны, она даёт более подробное представление, чем модель «чёрного ящика».

Сегодня мы узнали, что такое системный анализ, познакомились с такими моделями как модель «чёрного ящика» и модель «состава».