Можно ли делить процент на процент

В этом уроке разберем как складывать и вычитать проценты между собой.

Проценты можно складывать и вычитать только с самими процентами.

Сложение и вычитание процентов

Проценты складываются и вычитаются друг с другом как обычные числа.

• 1% + 37% − 25% = 38% − 25% = 13%
• 70% − (42% + 3%) = 70% − 45% = 25%

В повседневной жизни полезно знать разные формы выражения одного и того же изменения величин, сформулированных без процентов и с помощью процентов.

Например, увеличить в 2 раза, значит увеличить на 100% . Разберёмся, почему это так.

Пусть « x » — это 100% .

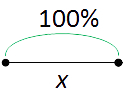
Тогда, увеличив « x » в 2 раза, получим « 2x ».

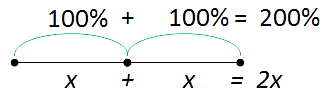
Сравним полученные результаты.

Получилось, что общее количество процентов равно 200% . Увеличить в 2 раза означает увеличить на 100% и наоборот.

Рассуждая, таким же образом, докажем, что увеличить на 50% , значит увеличить в 1,5 раза .

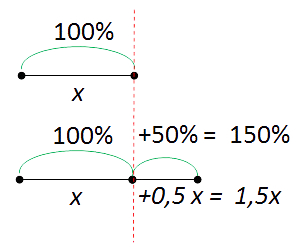
Уменьшение числа также может быть выражено в процентах.

Известно, что « x » уменьшилось на 80% . Найдём, во сколько раз уменьшилось « x ».

Вначале найдём, сколько процентов от x осталось.

20% осталось от « x ». Обозначим остаток « x » за « y ».

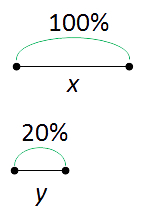
Составим пропорцию. По числовому коэффициенту определяем, во сколько раз уменьшился « x ».

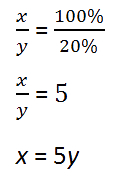
Таким образом, мы установили, что уменьшить на 80% , значит уменьшить в 5 раз.

Поняв связь между процентами и «разами», вы без труда сможете понимать о чём так часто говорят в новостях и в газетах, приводя различные статические данные.

Некоторые, наиболее употребимые фразы, желательно просто запомнить, чтобы всегда точно понимать о чём идёт речь. Список таких фраз представлен ниже.

Значение фраз «увеличить и уменьшить на … процентов»

Увеличить на 50% , значит увеличить в 1,5 раза.

• на 100% → в 2 раза
• на 150% → в 2,5 раза
• на 200% → в 3 раза
• на 300% → в 4 раза

Уменьшить на 80% , значит уменьшить в 5 раз.

• на 75% → в 4 раза
• на 50% → в 2 раза
• на 25% → в ≈ 1,33 раза
• на 20% → в 1,25 раза

Хочешь подготовиться к ОГЭ или ЕГЭ по математике на отлично?

Хочешь проверить свои силы и узнать результат насколько ты готов к ЕГЭ или ОГЭ?

Важное замечание!
Если вместо формул ты видишь абракадабру, почисти кэш. Как это сделать в твоем браузере написано здесь: «Как почистить кэш браузера».

Знаю: наверняка ты терпеть не можешь слово «процент». Но это чувство у тебя скоро исчезнет. Чтобы это произошло, разберем такой вопрос:

Что такое процент?

Откуда взялось это слово?

Все очень просто. Слово процент произошло от латинского per cent– на сотню, и означает оно «сотая доля» или «сотая часть». То есть один процент любого числа – это одна сотая этого числа.

И все. Этого достаточно, чтобы решать задачи, в которых присутствует это противное слово «процент».

Например: чему равны от числа ?

Прочтем это задание по-другому: чему равны сотых доли числа ? Элементарно, правда? Нужно разделить число на частей (чтобы узнать, чему равна одна сотая доля – один процент) и взять таких части:

Сколько процентов содержится в числе?

Снова перефразируем вопрос, заменив слово «процент» на «сотую часть»: Сколько сотых частей находится в числе? Ответ сразу становится очевидным: в любом числе или предмете находится ровно сто сотых частей (то есть, если разделить число или предмет на частей, сколько будет этих частей? Очевидно же, что ).

Разберем еще несколько примеров.

1. Чему равны от числа ?
2. Чему равно число, которого равны ?
3. Сколько процентов составляет число от числа ?

Решения:

1) И снова избавимся от слова «процент». Получим такой вопрос:

Чему равны сотых числа ?

Может показаться странным, что у нас целых – ведь мы уже выяснили, что в числе всего . Но с математической точки зрения ничего странного, ведь процент – это всего лишь одна сотая от числа. Почему нельзя одну сотую числа взять раз? Можно, ведь по сути это – просто число.

2) Итак, от числа равны . Можем составить простенькое уравнение:

Ты заметил, что я сразу же вместо написал ? И правда, один процент – это одна сотая, а значит, процентов – это сотых. Ты можешь тоже так делать.

3) Обозначим искомое количество процентов буквой . Тогда от числа равно . Или, что то же самое, сотых от числа равно :

Проценты и десятичные дроби

В разобранных выше примерах мы убедились, что вместо знака процента % можно писать , или просто разделить на . То есть, – это то же самое, что ; – это и так далее. Но ведь любую из этих дробей можно записать компактнее: в виде десятичной дроби.

Например:

Значит, проценты можно записать в виде десятичной дроби.

Правило перевода такое: сколько бы ни было процентов, смещаем десятичную запятую на два знака влево и убираем значок % – и таким образом получаем обычное число. Данное правило будем теперь всегда применять сразу.

Например:

1) Чему равны от числа ?

Вместо напишем что? . Итак, .

2) от какого числа равны ?

Изменение числа на сколько-то процентов

Когда говорят, что число увеличилось на , это значит, что к числу надо прибавить .

Если же число уменьшилось на , это значит, что из числа надо вычесть .

Рассмотрим пример:

Цена холодильника в магазине за год увеличилась на . Какой стала цена, если изначально холодильник стоил р?

Решение:

Для начала определим, на сколько рублей изменилась (в данном случае – увеличилась) стоимость холодильника. По условию – на . Но от чего? Конечно же, от самой начальной стоимости холодильника ( р). Получается, что нам нужно найти от р:

Теперь мы знаем, что цена увеличилась на р. Остается только, согласно правилу, прибавить к начальной стоимости величину изменения:

Новая цена рублей.

Еще пример (постарайся решить самостоятельно):

Книга «Математика для чайников» в магазине стоит р. Во время акции все книги продаются со скидкой . Сколько теперь придется заплатить за эту книгу?

Решение:

Что такое скидка, ты наверняка знаешь? Скидка в означает, что стоимость товара уменьшили на .

На сколько уменьшилась стоимость книги (в рублях)? Нужно найти от начальной ее стоимости в р:

Цена уменьшилась, значит нужно из начальной стоимости вычесть то, на сколько она уменьшилась:

Новая цена рублей.

Правда ведь просто?

Но есть способ сделать это решение еще проще и короче!

Рассмотрим пример:

Увеличьте число на .

Чему равны от ? Как мы уже выяснили раньше, это будет .

Теперь увеличим само число x на эту величину:

Получается, что в результате мы к десятичной записи прибавили и умножили на число . Обобщим это правило:

Пусть нам нужно увеличить число на .

Тогда новое число будет равно: .

Чтобы увеличить число на , нужно умножить его на .

Например, увеличим число на :

А теперь попробуй сам:

1. Увеличить число на
2. Увеличить число на
3. На сколько процентов число больше числа ?

Решения:

3) Пусть искомое количество процентов равно . Это значит, что если число увеличить на , получится :

Если число x надо уменьшить на , все аналогично:

Уменьшить число на какую-то величину – значит вычесть из него эту величину:

Чтобы уменьшить число на , нужно умножить его на .

Примеры:

1) Уменьшить число на .

2) На сколько процентов число меньше числа ?

3) Цена товара со скидкой в равна р. Чему равна цена без скидки?

Решения:

2) Число уменьшили на x процентов и получили :

3) Пусть цена без скидки равна . Получается, что x уменьшили на и получили :

Напоследок рассмотрим еще один тип задач, частенько вызывающих недоумение:

Число больше числа на . На сколько процентов число меньше числа ?

Что за странный вопрос: конечно же на ! Правильно?

А вот и нет. Если, например, масса одного шкафа на 25 кг больше массы другого, то, без сомнения, масса второго шкафа на 25 кг меньше массы первого. Но с процентами так не прокатит! Ведь в первом случае, когда говорим, что число на больше числа , мы считаем от числа ; а во втором случае, когда говорим, что число на меньше числа , мы считаем от числа . А поскольку числа и разные, то и от этих чисел будут разными!

Чтобы решить эту задачу верно, давай запишем условие в виде уравнения:

Число больше числа на . Это значит, что если число увеличить на , получим число :

Теперь в таком ж виде запишем вопрос: если число a уменьшить на процентов, получим число :

Выразим число из равенства (1):

И подставим в (2):

Отсюда следует, что:

Итак, получаем, что число на меньше числа !

Подобные задачи часто попадаются в ЕГЭ.

Например:

В понедельник акции компании подорожали на некоторое число процентов, а во вторник подешевели на то же самое число процентов. В результате они стали стоить на дешевле, чем при открытии торгов в понедельник. На сколько процентов подорожали акции компании в понедельник?

Решение:

Пусть цена акции в понедельник была равна , а искомое количество процентов, записанное в виде десятичной дроби (то есть, уже поделенное на ), равно .

Запишем формулой, чему равна стоимость акции после подорожания:

Далее, эту новую стоимость уменьшили на процентов:

При этом известно, что эта конечная цена на меньше начальной цены . То есть, если уменьшить на , получим :

Подставим , выраженное ранее:

Согласно здравому смыслу подходит только положительное решение:

Вспомним теперь, что это пока только десятичная запись искомого количества процентов, то есть это количество процентов, деленное на . Чтобы перевести в проценты, нужно домножить на 100%:

Где мы используем проценты в жизни?

Чаще всего мы их видим в банковских продуктах: вкладах, кредитах и т.д.

Если ты хорошо понимаешь, что такое проценты, и умеешь решать уравнения, то ты без труда расчитаешь, например, размер ежемесячного платежа по кредиту или сколько придётся переплатить, взяв ипотеку.

Такая задача есть в ЕГЭ под номером 17.

Но в жизни люди не любят считать сами и пользуются программами-калькуляторами для рассчета ипотечного кредита, которые делают точные расчёты автоматически.

Теперь ты можешь обойтись без них.

Заключение

Ну что же, теперь подведем итоги:

· Процент – это сотая часть, или одна сотая

· Решая задачи на проценты, старайся сразу избавляться от знака %, переводя проценты в десятичную дробь – число процентов нужно разделить на .

· Пользуйся упрощенными формулами, когда нужно увеличить или уменьшить число на сколько-то процентов: нужно домножить число на , если ты увеличиваешь его на , и на , если уменьшаешь.

Проценты – это легко! Удачи!

ПРОЦЕНТЫ. КОРОТКО О ГЛАВНОМ

Один процент любого числа – это одна сотая этого числа.

1. Проценты и десятичные дроби

2. Изменение числа на сколько-то процентов

Допустим, нужно увеличить число на .

Тогда, новое число будет равно: .

Чтобы увеличить число на , нужно умножить его на .

Если число надо уменьшить на , то :

Уменьшить число на какую-то величину – значит вычесть из него эту величину:

Чтобы уменьшить число на , нужно умножить его на .

Получить доступ к учебнику YouClever без ограничений можно кликнув по этой ссылке:

Процент на процент или капитализация процентов или сложная система процентов – это начисление процентов на сумму, по которой уже поступают проценты.

Как происходит начисление процентов на проценты?

Как известно, процент – это выплата определенной суммы денег, соразмерной вложенной или уставной сумме денег. Например, уставная сумма равна 1000 рублей, эта сумма положена под десять процентов. Десять процентов по-другому 0.1 от вложенной 1000 рублей. Перемножаем эти два числа и получаем сумму в 100 рублей, эта сумма и будет процентом по вкладу.

Данный метод называется методом простых процентов: мы просто взяли процент от числа и прибавили его к основному числу. Если анализировать данную теорию с математической точки зрения, то, принимая процент в долях за «x», а уставной капитал за «y», конечная сумма после процентного начисления «z» будет высчитываться по уравнению: z=y+y*x Таким образом, 1000+1000*0.1=1100.

Теперь разберем сложную систему начисления процентов. Допустим, денежная сумма была положена на определенный срок с условием, что по прошествии этого срока, клиент получит 10 процентов от суммы вклада, а по прошествии еще некоторого времени: 5% на сумму, уже выросшую в процентах.

Разберем эту ситуацию сначала просто на словах, а потом научимся записывать в уравнениях, чтобы вы могли при необходимости подставить любые цифры и высчитать прибыль. Итак, сначала по прошествии определенного срока на вклад будет начислен процент. Предположим, что вклад также равен 1000 рублей. Тогда 10 процентов от этого вклада, как мы уже писали выше, будет составлять 100 рублей. Когда закончится срок вложения, вкладчик будет иметь на своем счету 1100 рублей. Когда пройдет еще некоторое время, ему начислят 5 процентов на имеющуюся, то есть уже увеличенную сумму денег. Таким образом, несложно сделать подсчет: прибавляем пять процентов к имеющейся сумме в 1100 рублей, для этого умножаем 1100 на 0.05 и получаем в конечном результате сумму на вкладе в размере 1155 рублей.

Как записать этот расчет в виде уравнения, чтобы можно было подставлять в него любые другие цифры и считать без проблем? Для этого мы берем наше первичное уравнение z=y+y*x и меняем его. К полученной в уравнении первом прибыли мы должны взять еще некоторый процент (обозначим его как х1), после чего уравнение примет вид: z=(y+y*x)+(y+y*x)*х1.

Вспомните школьные годы, в математике обязательно были задачки на проценты, которые далеко не всем нравятся, потому что в них надо вникать.

Мы разобрали начисление процентов по сложной и простой схеме, теперь давайте узнаем, где используется сложная система процентов.

Где используется "процент на процент"?

Самое элементарное применение капитализации процента мы находим в банковской сфере. Банк начисляет проценты именно по сложной схеме. Таким образом, ежегодно положенный вклад будет увеличиваться согласно вышеприведенному уравнению.

Некоторое математики для иллюстрации системы начисления сложных процентов приводят в пример евангельскую притчу о бедной вдове, которая положила на храм две лепты – самое дорогое, что у нее было. Если положить две копейки в банк с начислением в пять процентов годовых по сложной системе, через 2012 лет сумма вклада составила бы 4.29*10 в сороковой степени рублей. Это конечно, просто расчеты, увы, деньги еще съедает инфляция, за 2012 лет ее процент был бы просто огромен, учитывая все происшедшее за эти годы события; могли происходить войны и так далее.

Еще сложная система процентов находит применение в кредитовании. Как правило, ее применяют к людям, которые не возвращают банку просроченные кредиты. Тогда банк ставит сложную систему процентов и начисляет процент на процент, многократно увеличивая сумму долга.

Исходя из всего вышесказанного, если вы разберетесь в функционировании данной системы, у вас практически никогда не будет проблем с финансовыми расчетами и балансовыми ведомостями. Удачи вам!