Может ли определенный интеграл быть отрицательным

Тема. Определенный интеграл

В общем виде определенный интеграл записывается так: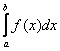

По сравнению с неопределенным интегралом прибавились пределы интегрирования.

Нижний предел интегрирования стандартно обозначается буквой .
Верхний предел интегрирования стандартно обозначается буквой .
Отрезок называется отрезком интегрирования.

Что такое определенный интеграл? Это ЧИСЛО.

Есть ли у определенного интеграла геометрический смысл? Есть.

Что значит решить определенный интеграл? Решить определенный интеграл – это значит, найти число.

Как решить определенный интеграл?С помощью формулы Ньютона-Лейбница:

Этапы решения определенного интеграла:

1) Сначала найти первообразную функцию 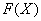(неопределенный интеграл). Константа в определенном интеграле никогда не добавляется. Запись является подготовкой для применения формулы Ньютона-Лейбница.

2) Подставить значение верхнего предела в первообразную функцию: .

3) Подставить значение нижнего предела в первообразную функцию: .

4) Рассчитать разность , то есть, найти число.

Всегда ли существует определенный интеграл? Нет, не всегда.

Например, интеграла не существует, поскольку отрезок интегрирования не входит в область определения подынтегральной функции (значения под квадратным корнем не могут быть отрицательными).

Что нужно, чтобы определенный интеграл существовал?Для того чтобы определенный интеграл существовал, необходимо чтобы подынтегральная функция была непрерывной на отрезке интегрирования.

Прежде чем приступить к решению ЛЮБОГО определенного интеграла, нужно убедиться в том, что подынтегральная функция непрерывна на отрезке интегрирования.

Может ли определенный интеграл быть равен отрицательному числу? Может.

Может ли нижний предел интегрирования быть больше верхнего предела интегрирования?Может.

– интеграл вычисляется по формуле Ньютона-Лейбница.

Некоторые свойства определенного интеграла.

1. В определенном интеграле можно переставить верхний и нижний предел, сменив при этом знак:

Например, в определенном интеграле перед интегрированием целесообразно поменять пределы интегрирования на «привычный» порядок:

– в таком виде интегрировать значительно удобнее.

2. Как и для неопределенного интеграла, для определенного интеграла справедливы свойства линейности:

– это справедливо не только для двух, но и для любого количества функций.

3. Для определенного интеграла справедлива формула интегрирования по частям:

Вычислить определенный интеграл

Решение: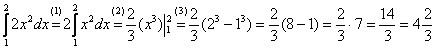

(1) Выносим константу за знак интеграла.

(2) Интегрируем по таблице с помощью формулы 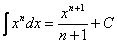. Появившуюся константу желательно отделить от и вынести за скобку.

(3) Используем формулу Ньютона-Лейбница . Сначала подставляем в верхний предел, затем – нижний предел. Проводим дальнейшие вычисления и получаем окончательный ответ.

Вычислить определенный интеграл

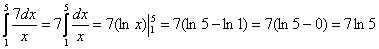
Вычислить определенный интеграл

Решение:

(1) Используем свойства линейности определенного интеграла.

(2) Интегрируем по таблице, при этом все константы выносим – они не будут участвовать в подстановке верхнего и нижнего предела.

(3) Для каждого из трёх слагаемых применяем формулу Ньютона-Лейбница:

Особое внимание обратите на третье слагаемое: –очень часто машинально пишут (особенно, когда подстановка верхнего и нижнего предела проводится устно и не расписывается так подробно). Еще раз внимательно изучите вышерассмотренный пример.

Следует заметить, что рассмотренный способ решения определенного интеграла – не единственный. Решение можно сократить:

Вычислить определенный интеграл

Решение:

Непосредственное вычисление определенного интеграла связано с трудностями – интегральные суммы имеют громоздкий характер и их трудно преобразовать к виду удобному для вычисления интегралов. По крайней мере, нет общих методов, как это сделать. Каждая задача решалась индивидуально, пока Ньютону и Лейбницу не удалось показать, что вычисление определенного интеграла от функции можно свести к отысканию ее первообразной.

Если функция f(x) непрерывна на отрезке [a,b] и функция F(x) является ее некоторой первообразной на этом отрезке, то имеет место формула Ньютона – Лейбница:

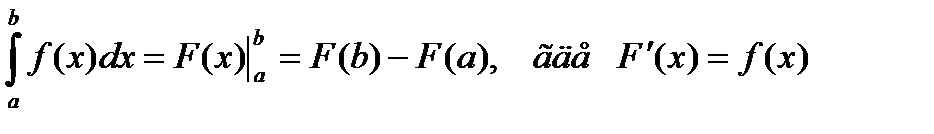, т.е. интеграл от дифференциала функции F(x) равен приращению этой функции на промежутке интегрирования.

Этапы решения определенного интеграла следующие:

1) Сначала находим первообразную функцию F(x) (неопределенный интеграл).

Замечание. Константа С в определенном интеграле никогда не добавляется. Обозначение 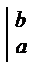является чисто техническим, и вертикальная палочка не несет никакого математического смысла, по сути – это просто отчёркивание.

2) Подставляем значение верхнего предела в первообразную функцию: F(b).

3) Подставляем значение нижнего предела в первообразную функцию: F(a).

4) Рассчитываем разность F(b)-F(a), то есть, находим число.

Всегда ли существует определенный интеграл? Нет, не всегда.

Например, интеграла 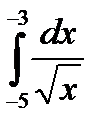не существует, поскольку отрезок интегрирования [-5;-2] не входит в область определения подынтегральной функции (значения под квадратным корнем не могут быть отрицательными). А вот менее очевидный пример: . Такого интеграла тоже не существует, так как в точках 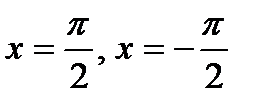отрезка [-2;3] не существует тангенса.

Для того чтобы определенный интеграл вообще существовал, необходимо чтобы подынтегральная функция быланепрерывной на отрезке интегрирования.

Из вышесказанного следует: перед тем, как приступить к решению ЛЮБОГО определенного интеграла, нужно убедиться в том, что подынтегральная функция непрерывна на отрезке интегрирования.

Может ли определенный интеграл быть равен отрицательному числу? Может. И отрицательному числу. И нулю. Может даже получиться бесконечность, но это уже будет несобственный интеграл.

Может ли нижний предел интегрирования быть больше верхнего предела интегрирования?Может, и такая ситуация реально встречается на практике.

Не нашли то, что искали? Воспользуйтесь поиском:

Лучшие изречения: Как то на паре, один преподаватель сказал, когда лекция заканчивалась – это был конец пары: "Что-то тут концом пахнет". 8516 – | 8100 – или читать все.

91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.

Отключите adBlock!
и обновите страницу (F5)
очень нужно

В общем виде определенный интеграл записывается так: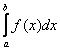

Что прибавилось по сравнению с неопределенным интегралом? Прибавились пределы интегрирования. Нижний предел интегрирования стандартно обозначается буквой 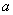. Верхний предел интегрирования стандартно обозначается буквой 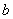. …и мы выполним все пункты от «а» до «бэ» =) (c) Отрезок 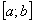называют отрезком интегрирования.

И перед тем, как перейдём к практике, небольшое faq по теме:

Что такое определенный интеграл? С формальной точки зрения, определённый интеграл – это ЧИСЛО. Да-да, самое что ни на есть обычное число:

Что значит решить определенный интеграл? Решить определенный интеграл – это значит, найти это число.

Как решить определенный интеграл? С помощью знакомой со школы формулы Ньютона-Лейбница: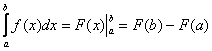

Формулу перепишите на листок и наклейте на самом видном месте!

Этапы решения определенного интеграла следующие:

1) Сначала находим первообразную функцию 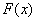(неопределенный интеграл). Обратите внимание, что константа 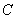в определенном интеграле не добавляется. Обозначение 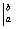является чисто техническим, и вертикальная палочка не несет никакого математического смысла, по сути – это просто отчёркивание. Зачем нужна сама запись 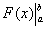? Подготовка для применения формулы Ньютона-Лейбница.

2) Подставляем значение верхнего предела в первообразную функцию: .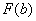

3) Подставляем значение нижнего предела в первообразную функцию: .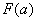

4) Рассчитываем (без ошибок!) разность 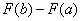. Готово.

Вопрос следующий, а на самом деле первый: всегда ли существует определенный интеграл? Нет, не всегда.

Например, интеграла 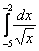не существует, поскольку отрезок интегрирования 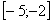не входит в область определения подынтегральной функции (значения под квадратным корнем не могут быть отрицательными). А вот менее очевидный пример: 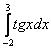. Такого интеграла тоже не существует, так как в точках 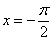, 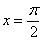отрезка 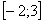не существует тангенса. Желающие могут сразу ознакомиться с Приложением Графики основных функций и их построение и оценить ситуацию геометрически: там, где нет графика – те значения и не входят в область определения той или иной функции.

Таким образом, чтобы определенный интеграл вообще существовал, нужно чтобы подынтегральная функция была непрерывной на отрезке интегрирования. Понятие непрерывности тоже интуитивно понятно – если график можно начертить, не отрывая карандаша от бумаги, то данная функция непрерывна на этом участке.

И из вышесказанного следует первая важная рекомендация: перед тем, как приступить к решению ЛЮБОГО определенного интеграла, желательно убедиться в том, что подынтегральная функция непрерывна на отрезке интегрирования.

В противном случае может получиться такой казус: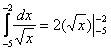
…что делать. – ведь нельзя же подставлять отрицательные числа под корень!

А сделать надо следующее: предварительно проверить функцию на непрерывность. И если для решения (в контрольной работе, на зачете, экзамене) вам предложен несуществующий интеграл вроде 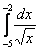или 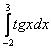, то нужно дать ответ, что интеграла не существует, и обосновать, почему. Хотя, не нужно. Скорее всего, это опечатка, и преподаватель может предложить вам корректный вариант, поэтому будет хорошей идеей сразу получить консультацию на этот счёт.

Может ли определенный интеграл быть равен отрицательному числу? Может. И отрицательному числу. И нулю. Может даже получиться бесконечность, но это уже будет несобственный интеграл, коим посвящена следующая глава.

Может ли нижний предел интегрирования быть больше верхнего предела интегрирования? Может, и такая ситуация реально встречается на практике:

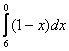– интеграл преспокойно вычисляется по формуле Ньютона-Лейбница.

Без чего не обходится математика? Конечно же, без всевозможных свойств:

Полную и свежую версию данного курса в pdf-формате ,
а также курсы по другим темам можно найти здесь.

Также вы можете изучить эту тему подробнее – просто, доступно, весело и бесплатно!

С наилучшими пожеланиями, Александр Емелин