Мат ожидание в экселе

Название работы: Расчет математического ожидания, среднего квадратического отклонения, дисперсии, с помощью программы Microsoft Excel

Категория: Лабораторная работа

Предметная область: Информатика, кибернетика и программирование

Описание: Так как функция математического ожидания это т оже самое что и функция среднего арифметического то: в пустой ячейке вводим = далее нажимаем fx выбираем функцию СРЗНАЧ выделяем числовые данные нашей исходной таблицы. Вычислить дисперсию: Вводим = далее fx Статистические ДИСП выделить числовые данные.

Дата добавления: 2014-02-08

Размер файла: 33.5 KB

Работу скачали: 269 чел.

Национальный Технический Университет Украины

„Киевский Политехнический Институт”

Факультет социологии и права

Лабораторная работа №2

Математические методы социологических исследований

„ Расчет математического ожидания, среднего квадратического отклонения, дисперсии, с помощью программы Microsoft Excel”

студент 2 курса

1. Вычислить математическое ожидание:

1) Пуск > Все программы > Microsoft Office > Microsoft Excel

2) Так как функция математического ожидания – это т оже самое, что и функция среднего арифметического, то: в пустой ячейке вводим «=», далее нажимаем fx, выбираем функцию СРЗНАЧ, выделяем числовые данные нашей исходной таблицы.

2. Вычислить дисперсию:

Вводим =, далее – fx, "Статистические" – "ДИСП", выделить числовые данные нашей исходной таблицы.

3. Среднее квадратичесое отклонение (не смещённое):

Вводим =, далее – fx, "Статистические" – "СТАНДТОТКЛОН", выделить числовые данные нашей исходной таблицы.

4. Среднее квадратическое отклонение (смещённое):

Вводим =, далее – fx, "Статистические" – "СТАНДТОТКЛОН", выделить числовые данные нашей исходной таблицы.

Вывод: Microsoft Excel является одной из самых удобных компьютерных программ, с помощью которых можно высчитать статические данные. В этом я убедился, когда высчитывал вышеуказанные данные.

Вычислим среднее значение выборки и математическое ожидание случайной величины в MS EXCEL.

Выборочное среднее

Среднее выборки или выборочное среднее (sample average, mean) представляет собой среднее арифметическое всех значений выборки.

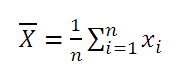
В MS EXCEL для вычисления среднего выборки можно использовать функцию СРЗНАЧ() . В качестве аргументов функции нужно указать ссылку на диапазон, содержащий значения выборки.

Выборочное среднее является «хорошей» (несмещенной и эффективной) точечной оценкой математического ожидания случайной величины (см. ниже), т.е. среднего значения исходного распределения, из которого взята выборка.

Примечание: О вычислении доверительных интервалов при оценке математического ожидания можно прочитать, например, в статье Доверительный интервал для оценки среднего (дисперсия известна) в MS EXCEL.

Некоторые свойства среднего арифметического:

• Сумма всех отклонений от среднего значения равна 0:

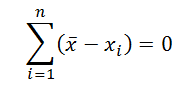
• Если к каждому из значений x_i прибавить одну и туже константу с, то среднее арифметическое увеличится на такую же константу;
• Если каждое из значений x_i умножить на одну и туже константу с, то среднее арифметическое умножится на такую же константу.

Математическое ожидание

Среднее значение можно вычислить не только для выборки, но для случайной величины, если известно ее распределение. В этом случае среднее значение имеет специальное название – Математическое ожидание. Математическое ожидание характеризует «центральное» или среднее значение случайной величины.

Примечание: В англоязычной литературе имеется множество терминов для обозначения математического ожидания: expectation, mathematical expectation, EV (Expected Value), average, mean value, mean, E[X] или first moment M[X].

Если случайная величина имеет дискретное распределение, то математическое ожидание вычисляется по формуле:

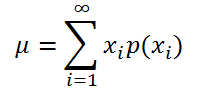
где x_i – значение, которое может принимать случайная величина, а р(x_i) – вероятность, что случайная величина примет это значение.

Если случайная величина имеет непрерывное распределение, то математическое ожидание вычисляется по формуле:

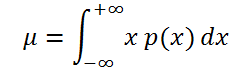
где р(x) – плотность вероятности (именно плотность вероятности, а не вероятность, как в дискретном случае).

Для каждого распределения, из представленных в MS EXCEL, Математическое ожидание можно вычислить аналитически, как функцию от параметров распределения (см. соответствующие статьи про распределения). Например, для Биномиального распределения среднее значение равно произведению его параметров: n*p (см. файл примера ).

События, характеризующие данные, могут носить случайный характер и появляться с разной вероятностью.

Вероятность события p есть отношение числа благоприятных исходов m к числу всех возможных исходов n этогособытия: p=m/n. Например, вероятность появления туза в наугад выбранной карте из колоды в 52 карты равна 4/52=0.0769, так как m=4, а n=52.

Если известно соответствие между появлениями (величинами) x₁, x₂, …, x_n случайного события (переменной) X и соответствующими вероятностями их реализации p₁, p₂, …, p_n, то говорят, что известен закон распределения случайной величины F(x). Большинство встречающихся на практике распределений вероятностей реализовано в Excel.

Распределения вероятностей имеют числовые характеристики.

Функции Excel для вычисления числовых характеристик распределения вероятностей. Они входят в группу Статистические. При вычислении функций в качестве случайных величин используйте следующие значения:

Математическое ожидание случайной величины (среднее арифметическое), характеризующее центр распределения вероятностей, вычисляется функцией СРЗНАЧ. СРЗНАЧ(A1:A7) = 9.

Дисперсия, характеризует разброс случайной величины относительно центра распределения вероятностей и вычисляется функцией ДИСПР. ДИСПР(A1:A7) = 4.857.

Среднеквадратичное отклонение есть квадратный корень из дисперсии, характеризует разброс случайной величины в единицах случайной величины и вычисляется функцией СТАНДОТКЛОНП. СТАНДОТКЛОНП(A1:A7) = 2.203893.

Квантиль случайной величины с законом распределения F(x) есть значение случайной величины x при заданной вероятности p., т.е. есть решение уравнения F(x)=p. Медиана есть квантиль с вероятностью p=0.5.

Excel, вместо квантилей содержит функции вычисления х для определенных уровней р: квартили (кварта – четверть), децили (дециль – десятая часть), персентили (персент – процент). Различают нижний квартиль с вероятностью p=0.25 и верхний квартиль с вероятностью p=0.75. Децили это квантили с вероятностью 0.1, 0.2, …, 0.9.

Функцию КВАРТИЛЬ используют, чтобы разбить данные на группы. В качестве второго аргумента указывают уровень (четверть), для которого нужно вернуть решение: 0 – минимальное значение распределения, 1 – первый, нижний квартиль, 2 – медиана, 3 – третий, верхний квартиль, 4 – максимальное значение. Например, КВАРТИЛЬ(A1:A7;3) = 10, т.е. 75% всех значений меньше 10, КВАРТИЛЬ(A1:A7;2) = 9.

Функция ПЕРСЕНТИЛЬ вычисляет квантиль указанного уровня вероятности и используется для определения порога приемлемости значений. В качестве второго аргумента указывают уровень 0.1, 0.2, …, 0.9. ПЕРСЕНТИЛЬ(A1:A7;0,9) = 11.8, т.е. 90% всех значений меньше 11.8.

Excel содержит инструмент Ранг и персентиль, который на основе набора данных формирует выходную таблицу, содержащую порядковый и процентный ранги для каждого значения в наборе данных. См. справку по F1. Ниже приведен пример установки надстройки Пактет анализа

Распределения вероятностей, реализованные в Excel.

Каждый закон распределения описывает процессы разной вероятностной природы и характеризуется специфическими параметрами:

– равномерное распределение – n случайных чисел выпадает с одной и той же вероятностью p=1/n; характеризуется нижней и верхней границей; примером является появление чисел 1, 2, …, 6 при бросании игральной кости (p=1/6);

– биномиальное распределение моделирует взаимосвязь числа успешных испытаний m и вероятностей успеха каждого испытания p при общем количестве испытаний n – функции БИНОМРАСП и КРИТБИНОМ;

– нормальное (гауссово) распределение описывает процессы, в которых на результат воздействует большое число независимых случайных факторов, среди которых нет сильно выделяющихся – функции НОРМРАСП, НОРМСТРАСП, НОРМОБР, НОРМСТОБР и НОРМАЛИЗАЦИЯ;

– распределение Пуассона, предсказывает число случайных событий на определенном отрезке времени или на определенном пространстве, позволяет аппроксимировать биномиальное распределение – функция ПУАССОН;

– экспоненциальное (показательное) распределение, моделирует временные задержки между событиями, описывает процессы в задачах массового обслуживания и в задачах с «временем жизни» – ЭКСПРАСП;

– распределение хи-квадрат, связано с нормальным, возвращает одностороннюю вероятность распределения и используется для сравнения предполагаемых и наблюдаемых значений – функция ХИ2РАСП;

– распределение Стьюдента, связано с нормальным, возвращает вероятность для t-распределения Стьюдента и используется для проверки гипотез при малом объеме выборки – функция СТЬЮДРАСП;

– F-распределение (Фишера), связано с нормальным и может быть использовано в F-тесте, который сравнивает степени разброса двух множеств данных – fраспобр;

– гамма-распределение используется для изучения случайных величин, имеющих асимметричное распределение, в теории очередей – функция ГАММАРАСП;

– а также другие распределения – функции БЕТАРАСП, ВЕЙБУЛЛ, ОТРБИНОМРАСП, ГИПЕРГЕОМЕТ, ЛОГНОРМРАСП и др.

Биномиальное распределениехарактеризуется числом успешных испытаний m, вероятностью успеха каждого испытания p и общим количеством испытаний n. Классическим примером использования биномиального распределения является выборочный контроль качества больших партий товара, изделий в торговле, на производстве, когда сплошная проверка невозможна. Из партии выбирают n образцов и регистрируют число бракованных m. Бракованными могут быть 1, 2, … , n образцов, но вероятности реального числа бракованных будут различными. Если контрольная вероятность брака ниже допустимой вероятности, то можно гарантировать достаточное качество всей партии.

В Excel функция БИНОМРАСП вычисляет вероятность отдельного значения распределения по заданным m, n и р, а функция КРИТБИНОМ – случайное число по заданной вероятности. Обычно функция КРИТБИНОМ используется для определения наибольшего допустимого числа брака.

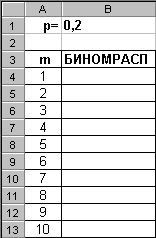
В качестве примера построим график плотности вероятности биномиального распределения для n=10 (1, 2, …, 10) и p=0.2. Введите исходные данные, как показано на рисунке:

Далее в ячейку В4 введите статистическую функцию БИНОМРАСП и заполните ее параметры как показано на рисунке:

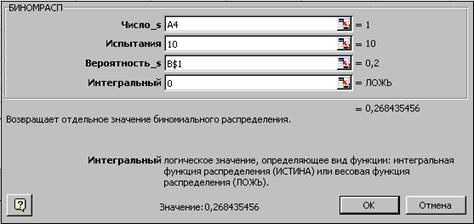
Здесь параметр Число_s есть число успешных испытаний m, Испытания – число независимых испытаний n, Вероятность_s – вероятность успеха каждого испытания p. Параметр Интегральный равен 0, если требуется получить плотность распределения (вероятность для значения m), и равен 1, если требуется получить вероятность с накоплением (вероятность того, что число успешных испытаний не меньше значения аргумента Число_s).

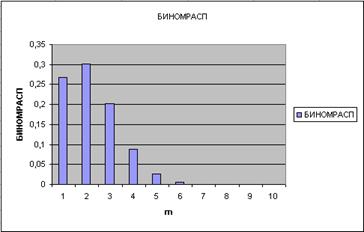
Формулу из В4 размножьте в ячейки В5:В13. Ниже показан результат:

В колонке В вычислены вероятности успешных испытаний m=1, 2, …, 10. Теперь по диапазону В4:В13 постройте график или гистограмму биномиальной функции плотности распределения – результат на рисунке. Поэкспериментируйте, изменяя значение вероятности в ячейке В1: 0.3, 0.4, 0.8, проследите за изменениями формы графика.

Для иллюстрации функции КРИТБИНОМ используем предыдущий пример – необходимо найти число m, для которого вероятность интегрального распределения больше или равна 0.75. Вызовите функцию КРИТБИНОМ и заполните параметры. Вы должны получить значение 3. Это означает, что при вероятности интегрального распределения >= 0.75 будет не менее трех (m>=3) успешных испытаний.

Нормальное распределениехарактеризуется средним арифметическим (математическим ожиданием) m и стандартным (среднеквадратичным) отклонением r. Дисперсия равна r 2 . Краткое обозначение распределения N(m,r 2 ). График нормального распределения симметричен относительно центра распределения (точки m), чем меньше r, тем больше вероятность появления случайной величины. В пределы [m-r,m+r] нормально распределенная случайная величина попадает с вероятностью 0,683 в пределы [m-2r,m+2r] – с вероятностью 0,955 и т.д.

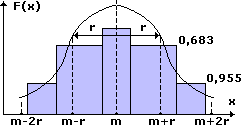
При m=0 и r=1 нормальное распределение называется стандартным или нормированным – N(0,1).

Нормальное распределение имеет очень широкий круг приложений. В качестве примера построим график плотности вероятностей нормального распределения при m=15 и r=1,5 в диапазоне [m-3r,m+3r] c шагом 0,5. Результат показан на рисунке.

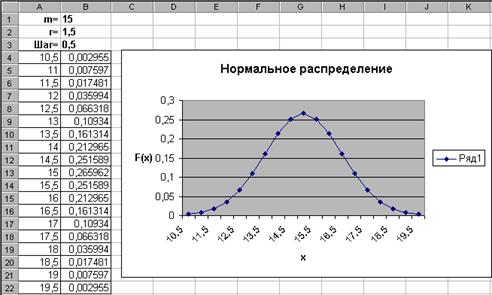
Выполните следующие действия:

– в ячейку А4 введите формулу =B1-3*B2, в ячейку А5 формулу =A4+B$3 и размножьте ее по ячейку А22;

– в ячейку В4 введите функцию НОРМРАСП из группы Статистические – параметры заполните как на рисунке;

– размножьте формулу из ячейки В4 по ячейку В22 и по диапазону В4:В22 постройте график; на 2-ом шаге мастера диаграмм в закладке Ряд введите подписи к оси х из диапазона А4:А22.