Можно ли теоретически рассчитать момент инерции блока
Лабораторная работа № 5
Определение моментов инерции тел произвольной формы
Цель работы
Определение момента инерции математического и физического маятника, а также изучение зависимости момента инерции физического маятника от распределения массы.
Теоретическая часть
Основное уравнение динамики вращательного движения тела вокруг неподвижной оси имеет вид:
 , (1)
, (1)
где  – векторная сумма моментов всех сил относительно оси вращения,
– векторная сумма моментов всех сил относительно оси вращения, 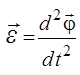 – угловое ускорение тела, т.е. вторая производная по времени от угла поворота φ тела. Соотношение (1) аналогично 2 – му закону Ньютона в динамике поступательного движения и в таком виде записывается в тех случаях, когда момент инерции тела при вращении не изменяется.
– угловое ускорение тела, т.е. вторая производная по времени от угла поворота φ тела. Соотношение (1) аналогично 2 – му закону Ньютона в динамике поступательного движения и в таком виде записывается в тех случаях, когда момент инерции тела при вращении не изменяется.
Моментом инерции материальной точки относительно некоторой оси называется величина, равная произведению массы точки на квадрат ее расстояния от оси вращения
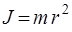 . (2)
. (2)
Для протяженных тел момент инерции определяется как сумма моментов инерции элементарных масс 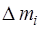 (материальных точек), на которые можно разбить тело:
(материальных точек), на которые можно разбить тело:
 . (3)
. (3)
Имеются различные методы экспериментального определения моментов инерции. В настоящей работе определение моментов инерции тел произвольной формы производится методом колебаний. Для этих целей измеряется период колебаний Т математического и физического маятников.
Математическим маятником называется материальная точка массой m, подвешенная на невесомой, нерастяжимой нити и совершающая колебания под действием силы тяжести.
Момент инерции математического маятника
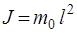 , (4)
, (4)
где l – длина маятника.
Период колебаний математического маятника определяется по формуле
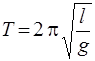 . (5)
. (5)
Физическим маятником называется твердое тело, совершающее колебания вокруг неподвижной горизонтальной оси, не совпадающей с его центром инерции, под действием силы тяжести.
 |
Если отклонить маятник от положения равновесия на угол φ (рис. 1), то момент силы, стремящийся вернуть маятник в положение равновесия равен
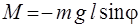 . (6)
. (6)
В (6) l – расстояние между точкой подвеса и центром инерции маятника С, m – масса маятника, 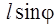 – плечо силы тяжести. Основное уравнение динамики вращательного движения (1) с учетом (6) можно записать в виде
– плечо силы тяжести. Основное уравнение динамики вращательного движения (1) с учетом (6) можно записать в виде
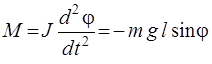 .
.
При малых углах отклонения 
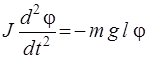 . (7)
. (7)
Уравнение (7) можно переписать в виде
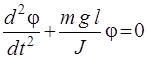 (8)
(8)
 . (9)
. (9)
Решение этого уравнения имеет вид
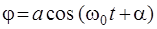 , (10)
, (10)
где а и α – произвольные постоянные. Через ω 2 обозначена величина
ω 2  . (11)
. (11)
Из уравнений (9) и (10) следует, что при малых отклонениях от положения равновесия физический маятник совершает гармонические колебания, частота которых зависит от массы маятника, момента инерции маятника относительно оси вращения и расстояния между осью вращения и центром инерции маятника. Зная ω, можно рассчитать период колебания Т физического маятника:
ω  ,
, 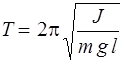 . (12)
. (12)
Из сопоставления формул (5) и (12) следует, что математический маятник длиной
 (13)
(13)
будет иметь такой же период колебаний, что и данный физический маятник. Величину  называют приведенной длиной физического маятника.
называют приведенной длиной физического маятника.
Точка на прямой, соединяющей точку подвеса с центром инерции, лежащая на расстоянии приведенной длины от оси вращения О, называется центром качания физического маятника О / .
По теореме Штейнера момент инерции тела относительно любой оси
 , (14)
, (14)
где 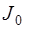 – момент инерции тела относительно оси, проходящей через центр тяжести, l – расстояние между осями.
– момент инерции тела относительно оси, проходящей через центр тяжести, l – расстояние между осями.
Подставим в уравнение (13) момент инерции, определяемый выражением (14):
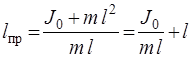 . (15)
. (15)
Из уравнения (15) видно, что приведенная длина всегда больше l, так что точка подвеса О и центр качания О / лежат по разные стороны от центра инерции С. Зная период колебания Т, массу маятника m и приведенную длину, можно рассчитать момент инерции J физического маятника:
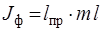 или
или 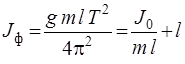 . (16)
. (16)
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Для студентов недели бывают четные, нечетные и зачетные. 9617 –  | 7511 –
| 7511 –  или читать все.
или читать все.
91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
| Название: Определение момента инерции твердых тел Раздел: Рефераты по физике Тип: лабораторная работа Добавлен 22:14:53 05 июня 2011 Похожие работы Просмотров: 1201 Комментариев: 14 Оценило: 3 человек Средний балл: 4.3 Оценка: неизвестно Скачать |
| Номер измерения | h1 =28,0 см | h2 =22,0 см | h3 =18,0 см | h4 =12,0 см | h5 =8,0 см |
| 1 | 3,617 | 3,281 | 3,092 | 2,348 | 1,986 |
| 2 | 3,73 | 3,23 | 2,891 | 2,346 | 1,921 |
| 3 | 3,797 | 3,414 | 3,133 | 2,521 | 2,099 |
| 4 | 3,597 | 3,414 | 3,061 | 2,323 | 2,058 |
| 5 | 3,837 | 3,238 | 2,882 | 2,412 | 2,096 |
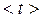 |
3,716 | 3,315 | 3,012 | 2,39 | 2,032 |
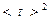 |
13,815 | 10,999 | 9,082 | 5,717 | 4,134 |
Из таблицы методического указания к лабораторному практикуму по физике А.Г. Риппа определим коэффициент Стьюдента.
Расчет погрешностей для построения графиков при коэффициенте
| Номер серии опытов |
Среднеквадра-тичное отклонение 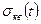 , с , с |
Случайная погрешность 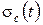 , с , с |
Абсолютная погрешность 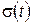 , с , с |
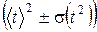 , с 2
, с 2
Определяем абсолютную систематическую приборную погрешность измерения времени согласно методическому указанию к лабораторному практикуму по физике А.Г. Риппа
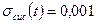 с.
с.
Метод наименьших квадратов для построения прямых по экспериментальным точкам :
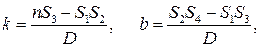
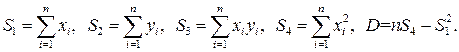
k= 0,49 с 2 /м угловой коэффициент прямой
b= 0,06 с 2 отрезок, отсекаемый прямой от оси OY
Искомая зависимость имеет вид: t 2 = 0,49∙ h , с 2 (4.1)
Вычислим значения ординат прямой линии для двух контрольных точек при произвольных значениях h по выражению 4.1:
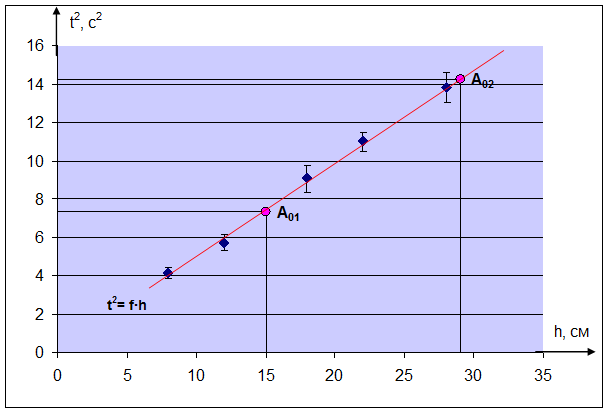
Рисунок 4.1. Зависимость квадрата времени t 2 от пройденного пути h
Погрешности косвенного измерения параметров прямой линии k и b методом наименьших квадратов определяются по следующим формулам:
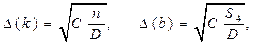

Используя выражение (3.7) для 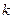 и учитывая, что
и учитывая, что 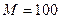 г,
г, 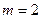 г, R = 75*10 -3 и g=980,67 см/с 2 вычисляется момент инерции
г, R = 75*10 -3 и g=980,67 см/с 2 вычисляется момент инерции 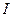 блока.
блока.
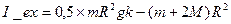 I_ex = 16986 г∙см 2
I_ex = 16986 г∙см 2
Абсолютная погрешности косвенного определения момента инерции блока I э в ходе эксперимента, по формуле:
 ∆(I_ex) = 552 г∙см 2
∆(I_ex) = 552 г∙см 2
Экспериментальное значение момента инерции блока:
I_ex = (16986 ± 552) г∙см 2 = (1,7 ± 0,6) × 10 -4 кг∙м 2
Используя геометрические параметры блока, с учетом плотности металла, из которого изготовлен блок (латунь, r = 8400 кг/м 3 ), рассчитать его момент инерции.
Толщина блока в метрах d= 6∙10 -3 м
Объём сплошного диска V_CD= π∙d∙R 2
Масса сплошного диска m_CD= p∙ V_CD
m_CD = 890 г = 0,89 кг
Момент инерции сплошного диска I_CD= 1/2∙ m_CD∙r2 2
I_CD = 25031 г∙см 2
Так как оси, проходящие через центры масс вырезанных дисков, не совпадают с осью вращения всего блока, то момент инерции I_can каждого диска находится по теореме Штейнера.
Радиус каждого выреза в метрах r2 = 30∙10 -3 м
Объём каждого выреза V_can= π∙d∙ r2 2
V_can= 1.696∙10 -5 см 3
Масса каждого вырезанного диска m_can= p∙V_can
m_can=142 г = 0,142 кг
Момент инерции каждого вырезанного диска относительно его центра масс:
Ic=1/2∙m_can∙ r2 2 Ic = 639 г∙см 2
r1 =40∙10 -3 м расстояние от оси вращения блока до центра масс каждого
вырезанного диска в метрах
Момент инерции каждого вырезанного диска относительно оси вращения блока:
I_can=Ic+ m_can∙ r1 2 I_can = 639 г∙см 2
Момент инерции цилиндрического отверстияI отв относительно оси, проходящей через центр масс блока, определяем по формуле:
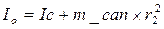 = 2911 г∙см 2
= 2911 г∙см 2
Момент инерции блока с тремя вырезами в виде малых дисков
I_an= I_CD-3∙ I_can I_an = 16298 г∙см 2
Полученные экспериментальным и аналитическим способами моменты инерции можно сравнить, получив отличие между ними в процентах, при помощи нижеследующего соотношения:
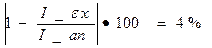
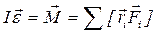 Используя экспериментальные данные, был построен график линеаризованной зависимости и рассчитаны коэффициенты соответствующего уравнения t 2 = f ( h ) = 0,49∙ h с 2 . Все точкив этой зависимостиукладываются на прямую в пределах их погрешностей.Это свидетельствует, что экспериментальная зависимость t 2 = f ( h ) соответствует теоретической, т.е. экспериментально доказана справедливость основного уравнения динамики вращательного движения:
Используя экспериментальные данные, был построен график линеаризованной зависимости и рассчитаны коэффициенты соответствующего уравнения t 2 = f ( h ) = 0,49∙ h с 2 . Все точкив этой зависимостиукладываются на прямую в пределах их погрешностей.Это свидетельствует, что экспериментальная зависимость t 2 = f ( h ) соответствует теоретической, т.е. экспериментально доказана справедливость основного уравнения динамики вращательного движения:
Значение собственного момента инерции,полученное в ходе эксперимента равно:
Используя геометрические параметры блока, с учетом плотности металла, из которого изготовлен блок, рассчитан его момент инерции:
Значение собственного момента инерции,полученное в ходе эксперимента, больше расчетного
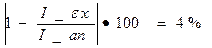
Несовпадение экспериментального результата с расчетным можно объяснить тем, что не учитывался момент сил трения. Это и привело к завышенному значению собственного момента инерции блока в эксперименте.
6. ОТВЕТЫ НА КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Что такое момент сил и момент инерции?
Моментом силы относительно оси называется физическая величина, численно равная произведению величины составляющей силы, действующей в плоскости, перпендикулярной оси вращения, на плечо этой составляющей, т.е. на кратчайшее расстояниеr от оси вращения до линии действия
Момент силы относительно оси есть вектор, направленный вдоль этой оси и связан с направлением вращения правилом правого винта.
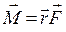
Момент инерции характеризует инерционные свойства вращающихся тел. Чем больше момент инерции тела, тем труднее изменить его угловую скорость. Момент инерции во вращательном движении аналогичен массе тела в поступательном движении. Момент инерции тела относительно некоторой оси зависит от распределения его массы относительно оси вращения.
Для элемента тела массой dm момент инерции dI выражается соотношением: dI = r 2 dm ,
где r – расстояние от элемента dm до оси вращения.
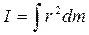 Момент инерции всего тела запишется в виде интеграла
Момент инерции всего тела запишется в виде интеграла
где интегрирование осуществляется по всему телу.
2. Моменты каких сил действуют на блок?
 Т1 и Т2 – силы натяжения нитей.
Т1 и Т2 – силы натяжения нитей.
На блок действуют моменты сил натяжения нитей:
Вращательное движение блока описывается уравнением:
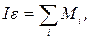 Рис. 6.1
Рис. 6.1
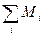 где ε – угловое ускорение блока, I – его момент инерции,
где ε – угловое ускорение блока, I – его момент инерции,
– сумма моментов сил, приложенных к блоку.
Согласно рис.6.1 вращательное движение блока описывается уравнением
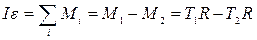
3. Как рассчитать момент инерции блока?
Сформулировать теорему Штейнера.
Момент инерции блока рассчитывается как:
где I диск – момент инерции сплошного диска;
I отв – момент инерции цилиндрического отверстия (“дырки”).
Момент инерции цилиндрического отверстияI отв относительно оси, проходящей через центр масс блока, определяем согласно теоремы Штейнера.
Момент инерции I относительно произвольной оси, равен сумме момента инерции I относительно оси, параллельной данной и проходящей через центр масс тела и произведения массы тела m на квадрат расстояния l между осями:
4. Укажите возможные причины несовпадения экспериментальных результатов с расчетными.
Физические допущения, принятые при теоретическом анализе движения грузов в эксперименте; погрешности измерения величин; точность вычислений.
Момент инерции блока с тремя вырезами в виде малых дисков
I_an= I_CD-3∙ I_can I_an = 16298 г∙см 2
Полученные экспериментальным и аналитическим способами моменты инерции можно сравнить, получив отличие между ними в процентах, при помощи нижеследующего соотношения:
Значение собственного момента инерции,полученное в ходе эксперимента равно:
Используя геометрические параметры блока, с учетом плотности металла, из которого изготовлен блок, рассчитан его момент инерции:
Значение собственного момента инерции,полученное в ходе эксперимента, больше расчетного
Несовпадение экспериментального результата с расчетным можно объяснить тем, что не учитывался момент сил трения. Это и привело к завышенному значению собственного момента инерции блока в эксперименте.
6. ОТВЕТЫ НА КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Что такое момент сил и момент инерции?
Моментом силы относительно оси называется физическая величина, численно равная произведению величины составляющей силы, действующей в плоскости, перпендикулярной оси вращения, на плечо этой составляющей, т.е. на кратчайшее расстояниеr от оси вращения до линии действия
Момент силы относительно оси есть вектор, направленный вдоль этой оси и связан с направлением вращения правилом правого винта.
Момент инерциихарактеризует инерционные свойства вращающихся тел. Чем больше момент инерции тела, тем труднее изменить его угловую скорость. Момент инерции во вращательном движении аналогичен массе тела в поступательном движении. Момент инерции тела относительно некоторой оси зависит от распределения его массы относительно оси вращения.
Для элемента тела массой dm момент инерции dIвыражается соотношением: dI = r 2 dm,
где r – расстояние от элемента dm до оси вращения.
где интегрирование осуществляется по всему телу.
2. Моменты каких сил действуют на блок?
На блок действуют моменты сил натяжения нитей:
Вращательное движение блока описывается уравнением:
– сумма моментов сил, приложенных к блоку.
Согласно рис.6.1 вращательное движение блока описывается уравнением
3. Как рассчитать момент инерции блока?
Сформулировать теорему Штейнера.
Момент инерции блока рассчитывается как:
где Iдиск – момент инерции сплошного диска;
Iотв – момент инерции цилиндрического отверстия (“дырки”).
Момент инерции цилиндрического отверстияIотв относительно оси, проходящей через центр масс блока, определяем согласно теоремы Штейнера.
Момент инерции Iотносительно произвольной оси, равен сумме момента инерции I относительно оси, параллельной данной и проходящей через центр масс тела и произведения массы тела m на квадрат расстояния l между осями:
4. Укажите возможные причины несовпадения экспериментальных результатов с расчетными.
Физические допущения, принятые при теоретическом анализе движения грузов в эксперименте; погрешности измерения величин; точность вычислений.
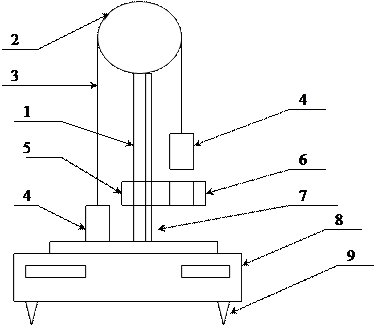
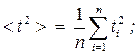
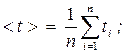
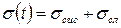
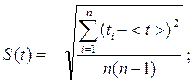
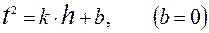 (3.7)
(3.7)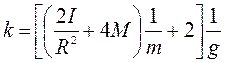 установки:
установки: